(School of Sciences,Jimei University,Xiamen 361021,China)
DOI: 10.6043/j.issn.0438-0479.202103007
备注
In this study,it is proved that finding N of a class of generalized biconic graphs can be converted into a calculation of a determinant of order 2.Based on this proof,explicit expressions for N of some special families of graphs are obtained,thus generalizing existing results.
引言
图的生成树数目一直是图论中较为热门的研究课题之一,计算图的生成树数目的方法有许多,其中较为著名的两个生成树计算方法为:Laplacian矩阵树定理和Feussner递推公式.迄今为止,已得到不少的图类的生成树数目的具体表达式,如:扇图[1-2]、轮图[1-2]、梯图[1-2]、基于圈或路的多重星[3]、双心轮图[4]、双柄扇图[4]等,其他关于图的生成树数目结果详见文献[5-9].
若T是图G=(V,E)的一个生成子图,同时T又是一棵树,则称T为图G的一棵生成树.每个连通图都包含生成树,若两棵生成树的边集不同,则这两棵生成树不同.设图G和H是两个顶点不相交的图,则G和H的联图,记为G∨H,是顶点集为V(G)∪V(H),边集为E(G)∪E(H)∪{uv|u∈V(G),v∈V(H)}的图.特别地,K1∨G和K2^-∨G分别称为G的锥图和双锥图,这里Kn表示n个顶点的完全图,Kn^-表示Kn的补图.本文考虑一类广义双锥图的生成树的数目,下面首先给出广义双锥图的定义.
定义1 设m为一个非负整数,设Km2是两个顶点(记为s1,s2)之间连m条边的图,G是顶点集为{v1,v2,…,vn}的一个图.给定两个非负整数向量α=(α1,α2,…,αn),β=(β1,β2,…,βn),在Km2和G的并图的基础上,分别在s1和vi之间连接αi条边,s2和vi之间连接βi(1≤i≤n)条边所得到的图,称为图G的一个广义双锥图,记为SG(m,α,β).(路P4的一个广义双锥图,如图1所示).
图1 SP4(2,α,β),α=(1,2,1,3),β=(2,2,1,2)
Fig.1 SP4(2,α,β),α=(1,2,1,3),β=(2,2,1,2)由上面的定义,很容易看出,当m=0,α=β=(1,…,1)=J时,SG(0,J,J)就是一般意义下的双锥图.本文主要考虑n个顶点路Pn的广义双锥图的生成树数目.陈东等[4]利用递归方法得到了SPn(0,J,J)(称为双柄扇图)生成树数目的具体表达式.本文将利用矩阵树定理得到一般SPn(m,α,β)的生成树数目的一个计算公式,在此基础上对参数取一些特殊值时,给出相应生成树数目的显式表达式,推广了文献[4]中的结果.
令G=(V,E)是n个顶点的图,图G的拉普拉斯矩阵为L(G)=D(G)-A(G),其中D(G)=diag(d1,d2,…,dn)是G的度对角矩阵,A(G)是G的邻接矩阵.则有如下著名的矩阵-树定理[10].
引理1 设G=(V,E)是n个顶点的图,L(G)是图G的Laplacian矩阵,M为L(G)的任意n-1阶子矩阵,则图G的生成树数目
τ(G)=|det(M)|.
特别地,对任意的s∈V(G),令L(G,s)表示由L(G)去掉s所对应的行和列得到的n-1阶子矩阵,则
τ(G)=det(L(G,s)).
1 广义双锥图SPn(m,α,β)的生成树数目
设广义双锥图SPn(m,α,β)的顶点集为{s1,v1,…,vn,s2},其中{v1,v2,…,vn}为路Pn的顶点集,α=(α1,α2,…,αn),β=(β1,β2,…,βn).为方便,记SPn=SPn(m,α,β),因此,SPn的Laplacian矩阵可以表示为:
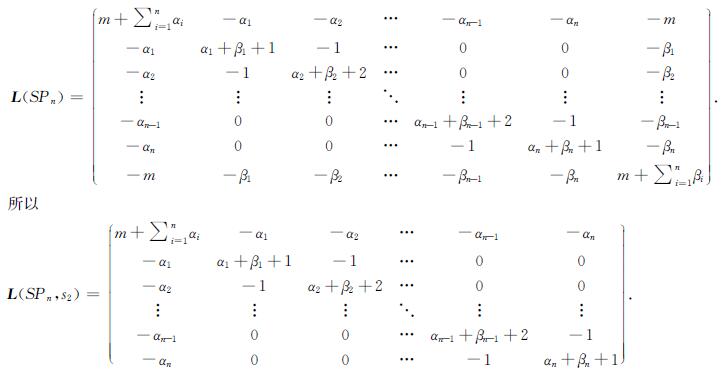
由引理1,马上可以得到下面的定理.
定理1 对广义双锥图SPn(m,α,β),其中m≥0,α=(α1,α2,…,αn),β=(β1,β2,…,βn).令ti=αi+βi+2,2≤i≤n-1,则
τ(SPn(m,α,β))=det(A-BD-1C),(1)
其中
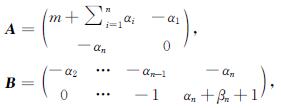
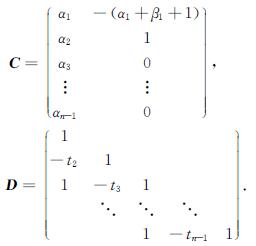
证明 由引理1,

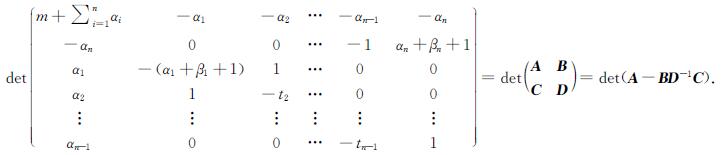
注意到,SPn(m,α,β)是平面图,对于图1所示的平面嵌入,其对偶图可以看做广义梯图(见图1的对偶图
Fig.2 Duel graph of fig.1">图2).众所周知,一个平面图的生成树数目等于其对偶图的生成树数目[10],所以式(1)也可以用来求广义梯图的生成树数目.式(1)是一个二阶行列式,对任意给定的参数m,n,α,β,由式(1)可以很快得到它的生成树数目.例1 对广义双锥图SP4(2,α,β),α=(1,2,1,3),β=(2,2,1,2),有
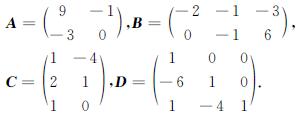
所以由式(1)计算得
τ(SG(2,α,β))=det(A-BD-1C)=2 723.
下一部分对一些特殊形式的参数α,β给出其生成树数目的具体表达式.
2 一些特殊广义双锥图SPn(m,α,β)的生成树数目
首先给出几个引理.
引理2 设n≥1,t是一个未定元,则n阶矩阵

可逆,且
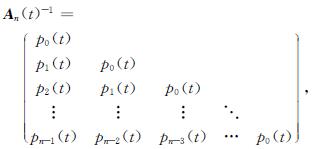
这里p0(t)=1,p1(t)=t,pk(t)=tpk-1(t)-pk-2(t),k≥2.
证明 直接验证An(t)An(t)-1=In.
求解pk(t)所满足的线性递归关系:
pk(t)=tpk-1(t)-pk-2(t),p0(t)=1,p1(t)=t.
很容易得到
pk(t)=1/(λ1-λ2)(λk+11-λk+12),(2)
其中
λ1=(t+(t2-4)1/2)/2,λ2=(t-(t2-4)1/2)/2.
由式(2)马上可以得到下面的结果.
引理3 令P^~k(t)=∑ki=0pi(t),k≥0,则有:
P^~k(t)=(pk+1(t)-pk(t)-1)/(t-2),(3)
且
∑nk=0P^~k(t)=(pn+1(t)-(n+2))/(t-2).(4)
证明 利用式(2)和等比数列求和公式可得.
由引理3和定理1,可以得到下面的结论.
定理2 设n≥4,α=(a,a,…,a),β=(c,b,…,b,c),pk(t),P^~k(t)(k≥0)定义同引理3.则
τ(SPn(m,α,β))=L1L3-L22,(5)
其中
L1=(a2)/(a+b)pn-1(t)+(nab)/(a+b)+m,
L2=a(t1P^~n-2(t)-P^~n-3(t)+1),
L3=t21pn-2(t)-2t1pn-3(t)+pn-4(t),
t=a+b+2,t1=a+c+1.
证明 既然α=(a,a,…,a),β=(c,b,…,b,c),式(1)中的A,B,C,D分别有如下形式:

然后由
τ(SPn(m,α,β))=det(A-BD-1C),
直接得到结论.
注:注意到pk(t)=tpk-1(t)-pk-2(t),且tP~k(t)-P^~k-1(t)+1=P^~k+1(t),所以式(5)中的L2和L3又可以表示为:
L2=a((t1-t)P^~n-2(t)+P^~n-1(t)),(6)
L3=(t1-t)2pn-2(t)+2(t1-t)pn-1(t)+pn(t).(7)
推论1 设n≥4,α=(a,a,…,a),β=(b,b,…,b),pk(t)定义如上.则
τ(SPn(m,α,β))=(nab+ma+mb)pn-1(t),(8)
其中t=a+b+2.
证明 令c=b代入定理2,即这时t1-t=-1,所以由式(6)和(7)得
L2=a(P^~n-1(t)-P^~n-2(t))=apn-1(t),
L3=pn-2(t)-2pn-1(t)+pn(t)=
(t-2)pn-1(t)=(a+b)pn-1(t).
然后由式(5)得
τ(SPn(m,α,β))=L1L3-L22=
((a2)/(a+b)pn-1(t)+(nab)/(a+b)+m)((a+b)pn-1(t))-
(apn-1(t))2=(nab+ma+mb)pn-1(t).
例2 图Pn∨K^-2和Pn∨K2的生成数目.
很显然Pn∨K^-2=SPn(0,J,J),Pn∨K2=SPn(1,J,J),所以由式(8)和(2)得
τ(Pn∨K2^-)=npn-1(4)=(31/2n)/6((2+31/2)n-
(2-31/2)n),
τ(Pn∨K2)=(n+2)pn-1(4)=
(31/2(n+2))/6[(2+31/2)n-(2-31/2)n].
上面的结果与文献[4]所得结果相一致.
推论2 设n≥4,α=(a,a,…,a),β=(b+1,b,…,b,b+1),pk(t)定义如上.则
τ(SPn(m,α,β))=(2a2)/((a+b)2)(pn(t)-
pn-1(t)-1)+((nab)/(a+b)+m)pn(t),(9)
其中t=a+b+2.
证明 令c=b+1代入定理2,这时t1-t=0,所以有
L2=aP^~n-1(t)=a(pn(t)-pn-1(t)-1)/(a+b),
L3=pn(t).
然后由式(5)和p2k-1(t)-pk-2(t)pk(t)=1,得
τ(SPn(m,α,β))=L1L3-L22=
((a2)/(a+b)pn-1(t)+(nab)/(a+b)+m)pn(t)-
(a/(a+b)(pn(t)-pn-1(t)-1))2=
(a2)/((a+b)2)[tpn-1(t)pn(t)-p2n(t)-p2n-1(t)+
2(pn(t)-pn-1(t))-1]+((nab)/(a+b)+m)pn(t)=
(2a2)/((a+b)2)(pn(t)-pn-1(t)-1)+
((nab)/(a+b)+m)pn(t).
- [1] 徐幼专.几类平面图生成树数目的一种求法[J].湖南科技学院学报,2006,27(5):17-18.
- [2] 王维凡,才德军.若干图类的生成树数[J].辽宁大学学报(自然科学版),1994(2):12-19.
- [3] 谭秋月.基于圈或路的多重星图和多重完全图相关图的生成树数目[D].厦门:厦门大学,2010.
- [4] 陈东,王维凡.一些图的生成树数[J].数学物理学报,2008,28(5):906-913.
- [5] YAN D M,JIANG S Q.Number of spanning trees of some simple graphs[J].Journal of Liaoning University,2007(3):250-252.
- [6] KELMANS A K.Transformations of a graph increasing its Laplacian polynomial and number of spanning trees[J].European Journal of Combinatorics,1997,18(1):35-48.
- [7] KELMANS A K.Spanning trees of extended graphs[J].Combinatorica,1992,12(1):45-51.
- [8] 赵继红,黎颖,张捷.一类平面图的生成树数目[J].湖南文理学院学报(自然科学版),2008,20(3):16-17,41.
- [9] 徐幼专,徐立新.利用对偶图求平面图的生成树数目[J].邵阳学院学报(自然科学版),2006(3):15-16.
- [10] BIGGS NORMAN.Algebraic graph theory[M].Cambridge:Cambridge University Press,1974:38-43-9.
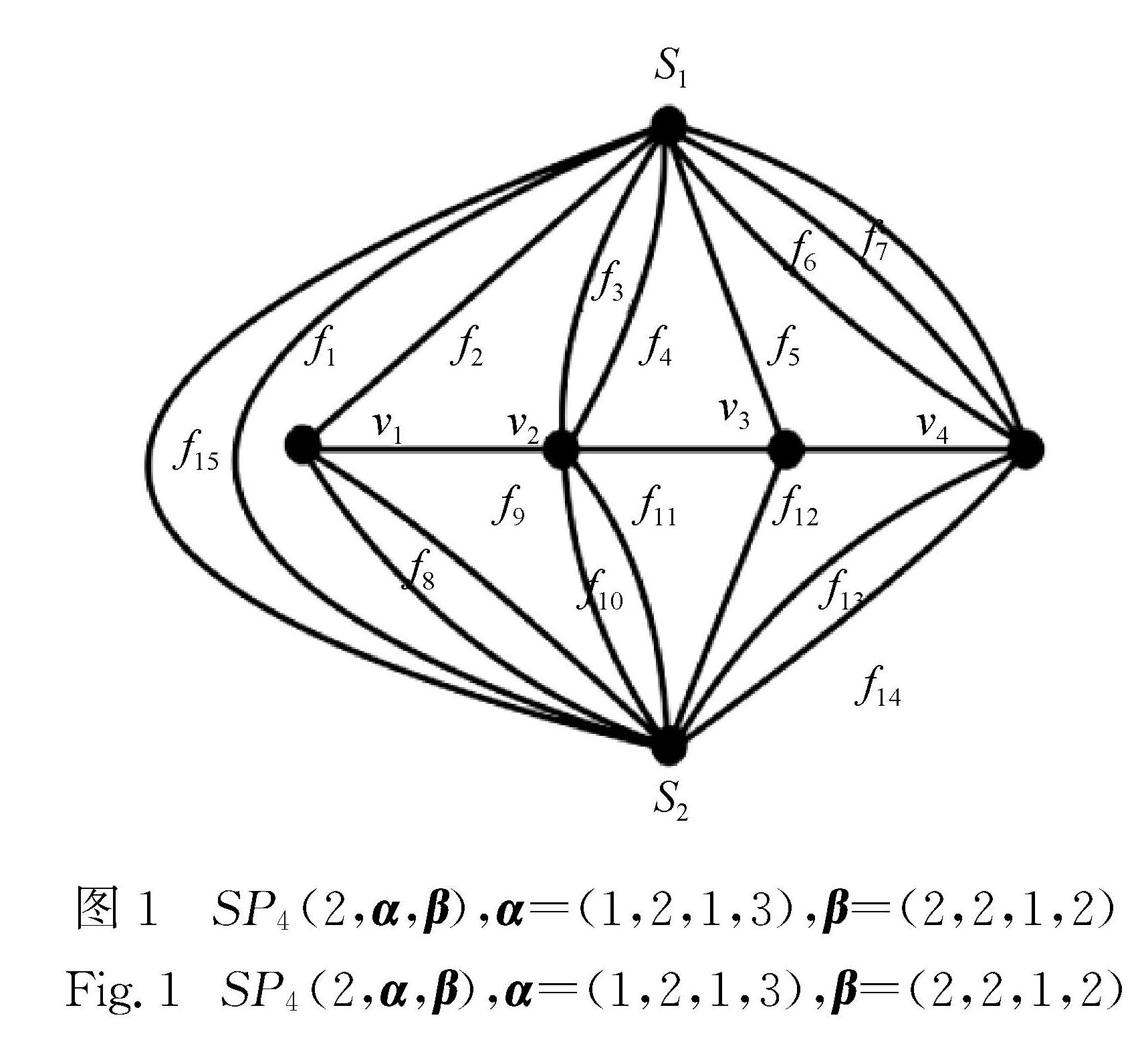
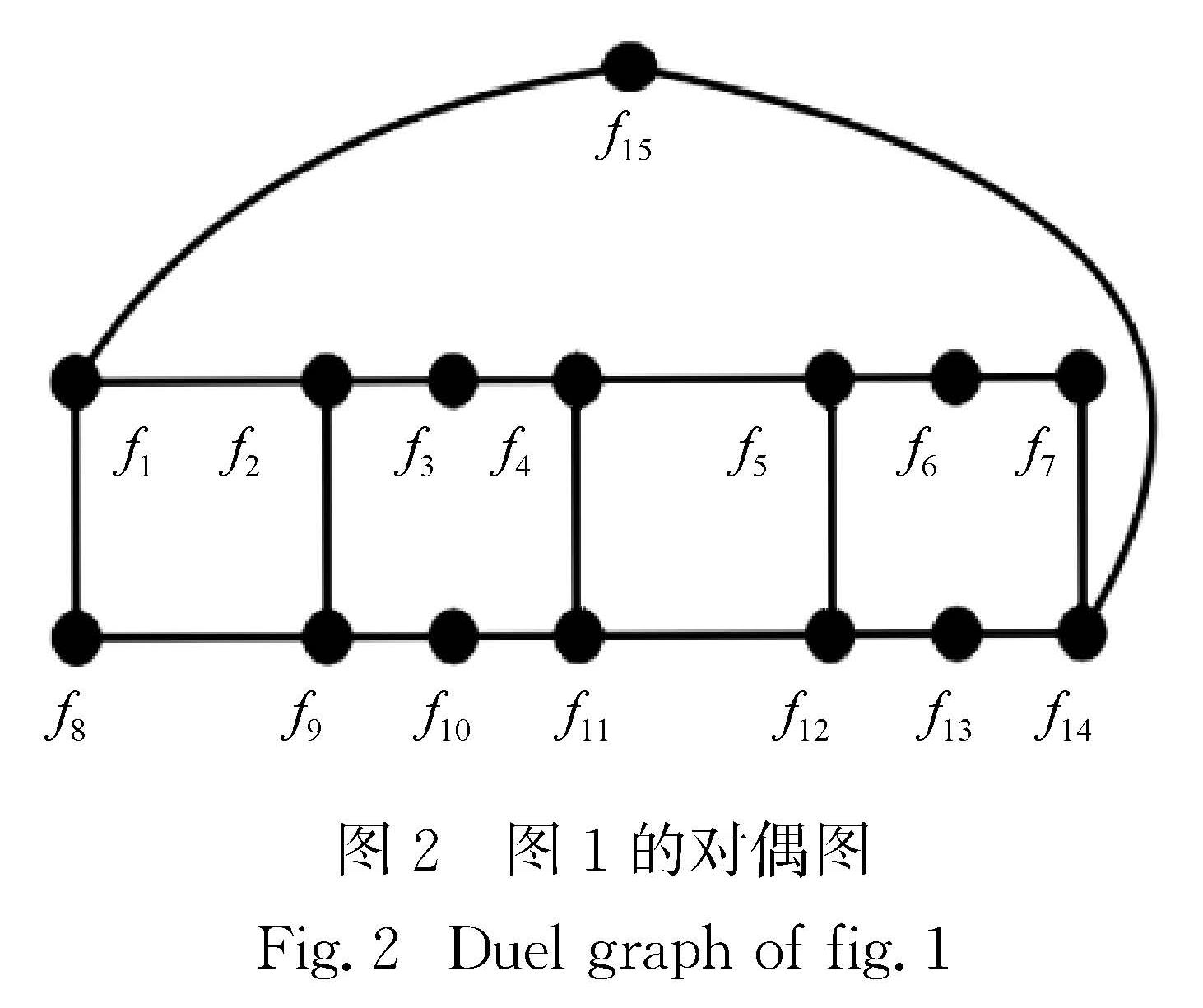 图1的对偶图
图1的对偶图