1 预备知识

本文研究了曾庆存院士^[1]提出的湿大气动力学方程组,证明了随机外强迫作用下湿大气动力学方程组初边值问题整体弱解的存在性和稳定性. 下面首先介绍湿大气方程组的初边值问题. 引入地形坐标系(θ,λ,ζ; t),θ是余纬且θ∈[0,π],λ是经度且λ∈[0,2π],p是气压且p∈[0,p_s],p_s为地表处气压,ζ=p/p_s∈[0,1],t表示时间. 那么,考虑如下随机外强迫作用的湿大气方程组.

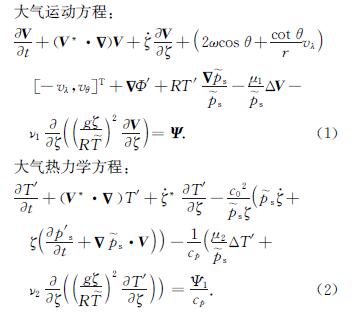
其中,C_o,C_p,R是热力学常数,u_i,v_i(i=1,2,3)是耗散系数,g是重力加速度,w是地球自转角速度,Ψ₁表示单位时间内大气从外界获得的热量,Ψ₂表示水汽相变过程中液态水的变化量.

该方程组的状态变量为水平速度场V、气压变化率ζ _·、温度偏差量T'、比湿q、重力位势偏差量Φ'、地表气压偏差量p'_s.T _～(ζ)为给定的参考标准温度,且满足T _～(ζ),T _～^-1(ζ)∈W^1,∞(0,1),T _～(ζ)>0,T _～(ζ)=O(ζ); p _～s(θ,λ)为给定的参考标准地球表面气压,且满足p _～s(θ,λ),p _～s^-1(θ,λ)∈W^1,∞([0,π]×[0,2π]:=S).

(V^*,ζ ^·*)是修正的光滑速度场,定义V^-:=∫¹₀V(θ,λ,ζ,t)dζ,采用

参考文献[2]中的方法,将p _～sV^-分解为p _～sV^-=Δχ+Δψ^⊥,可得V^*=V-p _～^-1_sΔχ=(v^*_θ,v^*_λ),ζ ^·*=-p _～^-1_s∫^ζ₀Δ·(p _～sV^*)ds,ds是地形坐标中垂直方向上一个微元,并且当ζ=1时,ζ ^·*=0.

参考文献[3-4]中的方法,可给出随机外强迫的定义.在完备的概率空间(Ω,F,P)中,假设ω₁,ω₂,ω₃,…是样本空间Ω中一列期望为E的独立标准的布朗运动,随机过程W是一个wiener过程,因此随机外强迫Ψ可定义如下:

Ψ=G(dW)/(dt)(6)

是关于时间的加性白噪声,而G是从(L²(Ω))²到(H^1+2γ₀(Ω))²(γ₀>0)的Hilbert-Schmidt算子.假设

Z(t)=∫^t_-∞e^-A₁(t-s)GdW(s)(7)

是满足以下随机Stokes方程初值问题

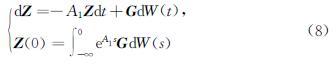
的解,这里A₁=-[(μ₁)/(p _～s)Δ+ν₁/(ζ)(((gζ)/(RT))²/(ζ))],是一个正Laplacian算子,且A₁的定义域为D(A₁)=H²(Ω)∩H¹₀(Ω),参照文献[3-4], 类似可得Z(t)是具有连续轨道的平稳遍历过程, 值在D(A^1+γ₁)中,其中γ<γ₀.

定义Ψ₁为非绝热加热作用,Ψ₂为水汽相变作用. 其余参数的含义可参见文献[1-2].

接下来,定义系统(1)～(5)的初边值条件. 首先,给定初值条件为

V|_t=0=V₀,T|_t=0=T₀, q|_t=0=q₀,(9)

再给出边界条件为

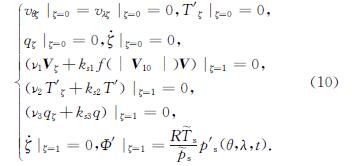
其中:所有关于θ的函数,均以π为周期; 所有关于λ的函数,均以2π为周期; k_s1、k_s2和k_s3均为正常数; V₁₀为给定函数,表示风速10 m/s,且满足V₁₀,V^-1₁₀∈L^∞(S); T _～s(θ,λ)为给定函数,表示地球表面标准温度,且满足T _～s(θ,λ)∈W^1,∞(S).关于初边值条件的物理意义可

参考文献[1,5].综合式(1)～(10),就得到了考虑随机外强迫作用的湿大气动力学方程组的初边值问题.

目前大气动力学方程组的适定性问题已经取得了很多重要成果. 例如,曾庆存^[5]就曾系统地论述过多种大气模式解的适定性,并提出了海气耦合问题. 随后,文献[2,6-15]研究了基于原始方程的各种大气动力学方程组,并证明了方程组初边值问题整体弱解和强解的适定性.另外文献[16-20]还研究了考虑水汽相变过程的湿大气方程组初边值问题的适定性.关于研究大气方程组吸引子的结论,可参见文献[11-12,14-17,21-22].

目前对考虑随机因素的大气方程组也有一些重要的结论. 例如,文献[23-25]中建立了随机气候模式和考虑随机外强迫作用的海气耦合模式. 之后,Griffies等^[26]和Majda等^[27-30]又对考虑随机外强迫作用的气候模式进行了数学理论和数值计算方面的研究.郭柏灵等^[3-4]还研究了考虑随机外强迫作用的海洋原始方程组的适定性以及整体吸引子的存在性等. 2018年,Dong等^[31]研究了具有指数混合性质的三维随机原始方程的适定性,得到了所有的弱解都有同一个不变测度,以及强解不变测度的唯一性.

首先,利用式(4)和(5),结合边界条件,可将考虑随机外强迫作用的湿大气动力学方程组简化为如下形式:

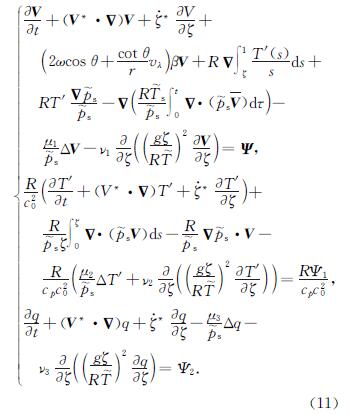
定义未知函数U:=(V,T',q),进而给定初值为

U|_t=0=(v_θ,v_λ,T',q)|_t=0=(v_θ0,v_λ0,T'₀,q₀)=

U₀,

边界条件为

{U(θ,λ,ζ)=U(θ+π,λ,ζ)=U(θ,λ+2π,ζ),

U_ζ|_ζ=0=0,

(ν₁V_ζ+k_s1f(∣V₁₀∣)V)|_ζ=1=0,

(ν₂T'_ζ+k_s2T')|_ζ=1=0,(ν₃q_ζ+k_s3q)|_ζ=1=0.

令u=V-Z(t),Z(t)是方程(8)的解,令U_～:=(u,T',q),则系统(11)可化为以下以U_～为未知量的新形式

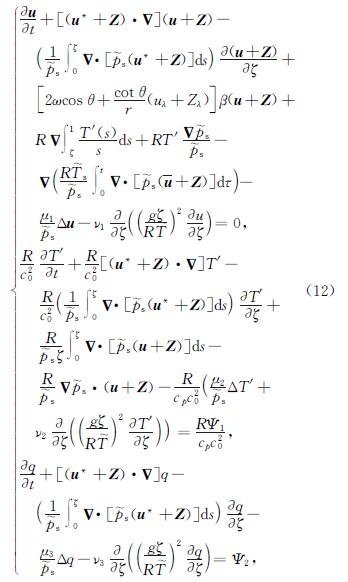
系统(12)满足如下边界条件:

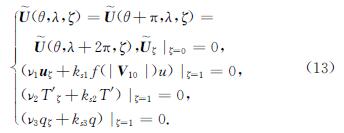
接下来定义如下算子:

B(U^～):=[u,R/(c²₀)T',q]^T,

F:=[0,R/(c²₀)Ψ₁,Ψ₂]^T,

D(U^～)(U^～):=

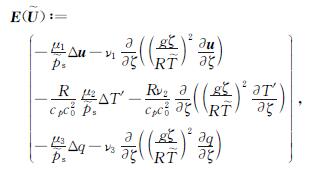
下面可给出类似于文献[2]中弱解的定义.

定义1(弱解的定义)对于任意的M>0,如果随机过程U_～(t,ω)=(u,T',q)满足U_～∈L^∞(0,M; L²(Ω))∩L²(0,M; H¹(Ω)), 并且在分布意义下,下述方程成立,

B(U_～)_t+D(U_～)(U_～)+E(U_～)=F,

即依概率对于几乎处处的ω∈Ω和任意试验函数φ=(φ₁,φ₂,φ₃)∈C^∞(0,M; C^∞₀(Ω)),使得

(B(U_～0),φ(0,·))_{p ～s}+∫^M₀(B(U_～),φ_t)_{p ～s}dt-

∫^M₀(b(U_～,φ)+c(U_～,φ)+e(U_～,U_～,φ)-

(F,φ)_{p ～s})dt=0,

其中,(·,·)表示在L²(Ω)上的内积,(·,·)_{p ～s}:=(p _～s·,·),b(U_～,φ)是耗散项在分布意义下得到的项,c(U_～,φ)是边界项在分布意义下得到的项,e(U_～,U_～,φ)是其余项在分布意义下得到的项,则U_～(t,ω)是系统(12)～(13)的弱解.

下面给出整体弱解的存在性和稳定性定理.

定理1(整体弱解的存在性)对于任意的M>0,设Ψ₁,Ψ₂∈L²(Ω×[0,M]),对于ω∈Ω,依概率几乎处处有Z∈L^∞(R; H¹(Ω))∩L²(R; H²(Ω))成立,且有U_～0∈L²(Ω),f(s)是正实数域上的单增连续函数,有正常数C₁、C₂使得C₁s^α≤f(s)≤C₂(1+s^α),其中α∈[0,1),则系统(12)～(13)存在整体弱解U_～,且满足

U_～∈L^∞(0,M; L²(Ω))∩L²(0,M; H¹(Ω)).

定理2(弱解的稳定性)对任意的M>0,若f(s)、Z、Ψ₁、Ψ₂满足定理1中的条件,假设系统(12)～(13)的一个整体弱解序列为U_～^m=(u^m,T'^m,q^m), 并假定初值序列为U_～^m|_t=0=(u^m,T'^m,q^m)|_t=0=U_～^m₀,再设U_～^m₀→U_～0∈L¹(Ω),其中U_～^m,U_～0∈L²(Ω),则存在子列,仍用U_～^m表示,有U_～^m→U_～∈L¹(0,T; L¹(Ω)),这里U_～是系统(12)～(13)以U_～0为初值的弱解.

注:借鉴

参考文献[2]中注2.2的方法,利用叶果洛夫定理可证明整体弱解的几乎处处稳定性,这里省略了具体的证明过程.

本部分给出系统(12)～(13)的能量估计.

引理1 在满足定理1的条件下,对任意的正数M,t∈[0,M],系统(12)～(13)的弱解U_～满足以下能量不等式

‖U_～‖²_L²(Ω)+∫^M₀‖U_～‖²_H¹(Ω)dt+

∫_S(RT _～s)/(p _～s)(∫^t₀Δ·(p _～su^-)dτ)²dσ+

∫^M₀∫_S(f(|V₁₀|)|u|²+T'²+q²)|_ζ=1dσdt≤

C(M).(14)

这里C(M)是与时间M有关的常数.

证明 令式(12)与(u,T',q)作内积,并利用边界条件得

1/2(d)/(dt)∫_Ωp _～s(u²+R/(c²₀)T'²+q²)dσdζ+1/2(d)/(dt)∫_S(RT _～s)/(p _～s)

[∫^t₀Δ·(p _～su^-)dτ]²dσ+∫_Ω(μ₁|Δu|²+

(μ₂R)/(c_pc²₀)|ΔT'|²+μ₃|Δq|²)dσdζ+∫_Ωp _～s

((gζ)/(RT ^～))²(ν₁|(u)/(ζ)|²+ν₂|(T')/(ζ)|²+ν₃|(q)/(ζ)|²)dσdζ+

∫_Sp _～s((gζ)/(RT ^～))²[f(|V₁₀|)|u|²+T'²+

q²]|_ζ=1dσ=I₁+I₂+I₃+I₄+I₅+

R/(c²₀c_p)∫_Ωp _～sT'Ψ₁dσdζ+∫_Ωp _～sqΨ₂dσdζ.

其中

I₁=∫_ΩR/(p _～s)Δp _～s·Z·(p _～sT')dσdζ-

∫_ΩR/ζ∫^ζ₀Δ·(p _～sZ)ds·(p _～sT')dσdζ,

I₂=-∫_Ωp _～su·([(u^*+Z)·Δ](u+Z)-

(1/(p _～s)∫^ζ₀Δ·[p _～s(u^*+Z)]ds)((u+Z))/(ζ))dσdζ,

I₃=-∫_Ωp _～sT'([(u^*+Z)·Δ]T'-

(1/(p _～s)∫^ζ₀Δ·[p _～s(u^*+Z)]ds)(T')/(ζ))dσdζ,

I₄=-∫_Ωp _～sq([(u^*+Z)·Δ]q-

(1/(p _～s)∫^ζ₀Δ·[p _～s(u^*+Z)]ds)(q)/(ζ))dσdζ,

I₅=-∫_ΩΔ((RT _～s)/(p _～s)(∫^t₀∫¹₀Δ·(p _～sZ)dζdτ))·

(p _～su)dσdζ-∫_Ω(2ωcos θ+(cot θ)/γ(u_λ+Z_λ)

β(u+Z)·(p _～u)dσdζ.

由Hölder不等式和Young不等式可得

|I₁|≤C‖Z‖_L²(Ω)‖T'‖_L²(Ω)+

C‖Z‖_H¹(Ω)‖T'‖_L²(Ω)≤C‖T'‖²_L²(Ω)+

C‖Z‖²_H¹(Ω),(15)

这里C表示某正常数,下同. 又因为

I₂=-∫_Ωp _～su·(u^*·Δ)udσdζ-∫_Ωp _～su·

(Z·Δ)udσdζ-∫_Ωp _～su·(u^*·Δ)Zdσdζ-

∫_Ωp _～su·(Z·Δ)Zdσdζ+

∫_Ωu·(∫^ζ₀Δ·(p _～su^*)dsu_ζ)dσdζ+

∫_Ωu·(∫^ζ₀Δ·(p _～sZ)dsu_ζ)dσdζ+

∫_Ωu·(∫^ζ₀Δ·(p _～su^*)dsZ_ζ)dσdζ+

∫_Ωu·(∫^ζ₀Δ·(p _～sZ)dsZ_ζ)dσdζ,(16)

且有

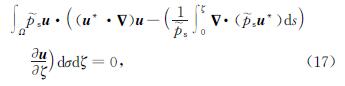
又由Hölder不等式、插值不等式和Young不等式可得

|∫_Ωp _～su·[(Z·Δ)u+(u^*·Δ)Z+(Z·Δ)Z]dσdζ|≤

C‖u‖_L⁴(Ω)‖Z‖_L⁴(Ω)‖Δu‖_L²(Ω)+

C‖u‖_L⁴(Ω)‖u^*‖_L⁴(Ω)‖ΔZ‖_L²(Ω)+

C‖u‖_L⁴(Ω)‖Z‖_L⁴(Ω)‖ΔZ‖_L²(Ω)≤

C‖u‖1/4L2(Ω)‖u‖</sup>7/4</sub>H1(Ω)‖Z‖L4(Ω)+</sub></sup>

C‖u‖1/2L2(Ω)‖u‖</sup>3/2</sub>H1(Ω)‖ΔZ‖L2(Ω)+</sub></sup>

C‖u‖3/4H1(Ω)(‖Z‖L4(Ω)‖u‖</sup>1/4</sub>L2(Ω))‖ΔZ‖L2(Ω)≤</sub></sup>

ε‖u‖²_H¹(Ω)+C(‖Z‖⁸_L⁴(Ω)+

‖Z‖⁴_H¹(Ω))‖u‖²_L²(Ω)+C‖Z‖²_H¹(Ω),(18)

这里ε是任意小的常数,下同. 另外由Hölder不等式、Minkowski不等式、插值不等式和Young不等式可得

|∫_Ωu·(∫^ζ₀Δ·(p _～sZ)ds u_ζ)dσdζ|≤∫_S[(∫¹₀u²dζ)^1/2

(∫¹₀|Δ·(p _～sZ)|dζ)(∫¹₀|u_ζ|²dζ)^1/2]dσ≤

(∫_S(∫¹₀|Δ·(p _～sZ)|dζ)⁴dσ)^1/4·

(∫_S(∫¹₀u²dζ)²dσ)^1/4(∫_S(∫¹₀|u_ζ|²dζ)dσ)^1/2≤

(∫¹₀‖Δ(p _～sZ)‖_L⁴(S)dζ)(∫¹₀‖u‖²_L⁴(S)dζ)^1/2·

(∫¹₀‖u_ζ‖²_L²(S)dζ)^1/2≤

C‖Z‖1/2H1(Ω)‖Z‖</sup>1/2</sub>H2(Ω)‖u‖</sup>3/2</sub>H1(Ω)‖u‖</sup>1/2</sub>L2(Ω)≤</sub></sup>

ε‖u‖²_H¹(Ω)+C‖Z‖²_H¹(Ω)‖Z‖²_H²(Ω)‖u‖²_L²(Ω),(19)

同理可得

|∫_Ωu·(∫^ζ₀Δ·(p _～su^*)dsZ_ζ)dσdζ|≤ε‖u‖²_H¹(Ω)+

C‖Z‖²_H¹(Ω)‖Z‖²_H²(Ω)‖u‖²_L²(Ω),(20)

|∫_Ωu·(∫^ζ₀Δ·(p _～sZ)dsZ_ζ)dσdζ|≤ε‖u‖²_H¹(Ω)+

C‖Z‖²_H¹(Ω)‖Z‖²_H²(Ω)‖u‖²_L²(Ω)+

C‖Z‖²_H¹(Ω),(21)

综合式(16)～(21)可得

|I₂|≤C(‖Z‖⁸_L⁴(Ω)+‖Z‖⁴_H¹(Ω))‖u‖²_L²(Ω)+

C‖Z‖²_H¹(Ω)+C‖Z‖²_H¹(Ω)‖Z‖²_H²(Ω)‖u‖²_L²(Ω)+

ε‖u‖²_H¹(Ω).

由分部积分可得I₃=0,I₄=0, 进一步由Hölder不等式和Young不等式可得

|I₅|≤ε‖Δu‖²_L²(Ω)+C+C‖u‖²_L²(Ω)+

C‖Z‖⁴_H¹(Ω)+C(M)∫^t₀‖Z‖²_H¹(Ω)dτ,

R/(c²₀c_p)∫_Ωp _～sT'Ψ₁dσdζ+∫_Ωp _～sqΨ₂dσdζ≤

C‖T'‖²_L²(Ω)+C‖Ψ₁‖²_L²(Ω)+C‖q‖²_L²(Ω)+

C‖Ψ₂‖²_L²(Ω),

综上可得

1/2(d)/(dt)∫_Ωp _～s(u²+R/(c²₀)T'²+q²)dσdζ+

1/2(d)/(dt)∫_S(RT _～s)/(p _～s)(∫^t₀Δ·(p _～su^-)dτ)²dσ+

∫_Ω(μ₁|Δu|²+(μ₂R)/(c_pc²₀)|ΔT'|²+μ₃|Δq|²)dσdζ+

∫_Ωp _～s((gζ)/(RT ^～))²(ν₁|(u)/(ζ)|²+ν₂|(T')/(ζ)|²+

ν₃|(q)/(ζ)|²)dσdζ+(∫_Sp _～s((gζ)/(RT ^～))²(f(|V₁₀|)·

|u|²+T'²+q²)|_ζ=1)dσ≤

C(‖Ψ₁‖²_L²(Ω)+‖Ψ₂‖²_L²(Ω)+‖Z‖²_L²(Ω))+

C(M)∫^t₀‖Z‖²_H¹(Ω)dτ+C‖Z‖²_H¹(Ω)+

C(1+‖Z‖⁸_L⁴(Ω)+‖Z‖⁴_H¹(Ω)+

‖Z‖²_H¹(Ω)‖Z‖²_H²(Ω))(‖u‖²_L²(Ω)+

‖T'‖²_L²(Ω)+‖q‖²_L²(Ω)).

对上式使用Gronwall不等式,即可证明式(14)成立.

本章将利用Faedo-Galerkin方法来证明系统弱解的存在性,选取{λ_j}是空间H¹₀(Ω)的完备正交基,设U_～^k=(u^k,T^k,q^k)是系统(12)的近似解,类似于文献[11-12], 则可得到近似解U_～^k=∑^k_i=1α_i,k(t)λ_i,α_ik(t)∈L²_loc(0,M; H¹(Ω)),并且满足以下方程:

(U_～^k'(t),λ_j)_{p ～s}-b(U_～^k(t),λ_i)-c(U_～^k(t),λ_i)-

e(U_～^k(t),λ_i)-(F,λ_i)_{p ～s}=0,

U_～^k(0)=∑^k_i=1(U_～0,λ_i)_{p ～s}λ_i.

由引理1可知近似解序列U_～^k(t)存在子列,为了方便,子列仍用U_～^k(t)表示,并且满足U_～^k(t)∈L^∞(0,M; L²(Ω))∩L²(0,M; H¹(Ω)),易知U_～^k(t)在L^∞(0,M; L²(Ω))中弱*收敛,在L²(0,M; H¹(Ω))中弱收敛. 设U_～为近似解序列的极限,只要证明U_～^k依L²(Ω)范数收敛到U_～,即可证明U_～也是系统的弱解. 下面证明U_～^k(t)的收敛问题,先给出以下引理.

引理2 设系统(12)～(13)的近似解序列为U_～^k,则U_～^k存在子列,子列仍用U_～^k表示,且满足

U_～^k→U_～∈L²(0,M; L²(Ω)),(22)

和

|∫^M₀(B(U_～^k),φ_t)_{p ～s}dt-∫^M₀(B(U_～),φ_t)_{p ～s}dt|→

0,(23)

其中,试验函数φ=(φ₁,φ₂,φ₃)∈C^∞(0,M; C^∞₀(Ω)),且满足φ(M,·)=0.

证明 利用式(12)与φ=(φ₁,φ₂,φ₃)∈H²₀(Ω)作内积,可得

(D(U_～^k)(U_～^k),φ)_{p ～s}=J₁+J₂+J₃+

∫_Ω(R∫¹_ζ(ΔT'^k(s))/sds·p _～sφ₁+R/ζ∫^ζ₀Δ·

[p _～s(u^k+Z)]ds·φ₂)dσdζ+

R∫_Ω(Δp _～sT'^kφ₁-Δp _～s·(u^k+Z)φ₂)dσdζ-

∫_ΩΔ((RT _～s)/(p _～s)∫¹₀∫^t₀Δ·[p _～s(u^k+Z)]dτdζ)·

p _～sφ₁dσdζ,

其中

J₁=∫_Ω[(u^*k+Z)·Δ](u^k+Z)·p _～sφ₁+

R/(c²₀)[(u^*k+Z)·Δ]T'^k·p _～sφ₂+

[(u^*k+Z)·Δ]q^k·p _～sφ₃dσdζ,

J₂=-∫_Ω(∫^ζ₀Δ·[p _～s(u^*k+Z)]ds).

(((u^k+Z))/(ζ)·φ₁+(T'^k)/(ζ)φ₂+(q^k)/(ζ)φ₃)dσdζ,

J₃=∫_Ω[2ωcos θ+(cot θ)/r(u^k_λ+Z_λ)]β(u^k+Z)·

p _～sφ₁dσdζ,

在下面的证明过程中,对于不含Z的项,可利用类似

参考文献[2]中引理4.2的证明方法得到,这里略去具体证明过程. 那么首先给出J₁的先验估计

J₁=∫_Ω(u^*k·Δ)u^k·p _～sφ₁dσdζ+∫_Ω(u^*k·Δ)Z·

p _～sφ₁dσdζ+∫_Ω(Z·Δ)u^k·p _～sφ₁dσdζ+

∫_Ω(Z·Δ)Z·p _～sφ₁dσdζ+R/(c²₀)∫_Ω(u^*k·Δ)T'^k·

p _～sφ₂dσdζ+R/(c²₀)∫_Ω(Z·Δ)T'^k·p _～sφ₂dσdζ+

∫_Ω(u^*k·Δ)q^k·p _～sφ₃dσdζ+∫_Ω(Z·Δ)q^k·

p _～sφ₃dσdζ,

下面以∫_Ω(u^*k·Δ)Z·p _～sφ₁dσdζ为例,来处理包含Z的项.由Hölder不等式可得

∫_Ω(u^*k·Δ)Z·p _～sφ₁dσdζ≤

C‖u^*k‖_H¹(Ω)‖Z‖_H¹(Ω)‖φ₁‖_H¹(Ω)≤

C‖U_～^k‖_H¹(Ω)+C,

同理可得

∫_Ω(Z·Δ)Z·p _～sφ₁dσdζ≤C,

∫_Ω[(Z·Δ)u^k·p _～sφ₁+R/(c²₀)(Z·Δ)T'^k·p _～sφ₂+

(Z·Δ)q^k·p _～sφ₃]dσdζ≤

C‖U_～^k‖_H¹(Ω)‖φ‖_H²(Ω)≤C‖U_～^k‖_H¹(Ω).

综合可得J₁≤C+C‖U_～^k‖_H¹(Ω),又有

J₂=-∫_Ω∫^ζ₀Δ·(p _～su^*k)ds((u^k)/(ζ)·φ₁+(T'^k)/(ζ)φ₂+

(q^k)/(ζ)φ₃)dσdζ-∫_Ω∫^ζ₀Δ·(p _～sZ)ds((u^k)/(ζ)·φ₁+

(T'^k)/(ζ)φ₂+(q^k)/(ζ)φ₃)dσdζ-∫_Ω∫^ζ₀Δ·(p _～su^*k)ds(Z)/(ζ)·

φ₁dσdζ-∫_Ω∫^ζ₀Δ·(p _～sZ)ds(Z)/(ζ)·φ₁dσdζ,

其中,由分部积分、Hölder不等式、Minkowski不等式和插值不等式可得

-∫_Ω∫^ζ₀Δ·(p _～sZ)ds((u^k)/(ζ)·φ₁+(T'^k)/(ζ)φ₂+

(q^k)/(ζ)φ₃)dσdζ≤C‖Z‖_H¹(Ω)(∫_Ω|U_～^k|³dσdζ)^1/3

(‖φ‖_L⁶(Ω)+‖φ_ζ‖_L⁶(Ω))≤

C‖U_～^k‖1/2H1(Ω)‖U～k‖</sup>1/2</sub>L2(Ω),</sub></sup>

同理可得

-∫_Ω∫^ζ₀Δ·(p _～su^*k)ds(Z)/(ζ)·φ₁dσdζ≤C+

C‖U^～k‖_H¹(Ω),

-∫_Ω∫^ζ₀Δ·(p _～sZ)ds(Z)/(ζ)·φ₁dσdζ≤C,

因此J₂≤C+C‖U_～^k‖3/2H1(Ω)‖U～k‖</sup>1/2</sub>L2(Ω)+C‖U～k‖</sup>1/2</sub>H1(Ω)‖U～k‖</sup>1/2</sub>L2(Ω)+C‖U～k‖H1(Ω),又有</sub></sup>

J₃=∫_Ω(2ωcos θ+(cot θ)/ru^k_λ)(u^k_θp _～sφ_1λ-

u^k_λp _～sφ_1θ)dσdζ+∫_Ω(2ωcos θ+(cot θ)/ru^k_λ)(Z_θp _～sφ_1λ-

Z_λp _～sφ_1θ)dσdζ+∫_Ω(2ωcos θ+(cot θ)/rZ_λ)(u^k_θp _～sφ_1λ-

u^k_λp _～sφ_1θ)dσdζ+∫_Ω(2ωcos θ+(cot θ)/rZ_λ)(Z_θp _～sφ_1λ-

Z_λp _～sφ_1θ)dσdζ,

其中,由Hölder不等式可得

∫_Ω(2ωcos θ+(cot θ)/ru^k_λ)(Z_θp _～sφ_1λ-Z_λp _～sφ_1θ)dσdζ≤

C(1+‖U_～^k‖_L²(Ω))(‖Z‖_L³(Ω)‖φ‖_L⁶(Ω))≤

C(1+‖U_～^k‖_L²(Ω)),

∫_Ω(2ωcos θ+(cot θ)/rZ_λ)(u^k_θp _～sφ_1λ-u^k_λp _～sφ_1θ)dσdζ≤

C‖U_～^k‖_L²(Ω),

∫_Ω(2ωcos θ+(cot θ)/rZ_λ)(Z_θp _～sφ_1λ-Z_λp _～sφ_1θ)dσdζ≤

C.

这里,(Z_θ,Z_λ)是向量Z的分量,因此J₃≤C+C‖U_～^k‖_H¹(Ω).

最后,由Hardy不等式和Hölder不等式可得

∫_ΩR/ζ∫^ζ₀Δ·(p _～sZ)ds·φ₂dσdζ≤C‖1/ζ∫^ζ₀Δ·

(p _～sZ)ds‖_L²(Ω)‖φ‖_L²(Ω)≤C‖Z‖_H¹(Ω)≤C,

-R∫_ΩΔp _～s·(u^k+Z)φ₂dσdζ≤C‖(u^k+

Z)‖_L²(Ω)‖φ₂‖_L²(Ω)≤C+C‖U_～^k‖_L²(Ω),

-∫_ΩΔ((RT _～s)/(p _～s)∫¹₀∫^t₀Δ·[p _～s(u^k+Z)]dτdζ)·

p _～sφ₁dσdζ≤C∫^t₀‖U_～^k‖_H¹(Ω)dτ+

C∫^t₀‖Z‖_H¹(Ω)dτ,

利用上述结论和

参考文献[2]引理4.2的证明方法可得

D(U_～^k)(U_～^k)∈L^4/3(0,M; H^-2(Ω)),E(U_～^k),

F∈L²(0,M; H^-2(Ω)),

因此,由方程(12)₁ 可得U_～^k_t∈L^4/3(0,M; H^-2(Ω)),再由U_～^k∈L²(0,M; H¹(Ω))和Aubi-Lions引理可得U_～^k→U_～∈L²(0,M; L²(Ω)),从而得到式(23)成立.

再借鉴文献[11-12]的证明思路,可得到系统(12)～(13)整体弱解的存在性,即定理2.1成立,这里不再给出具体证明过程.

接下来,证明系统(12)～(13)整体弱解的稳定性.

通过能量估计(14),可知弱解序列U_～^m满足一定的正则性条件,即

U_～^m∈L^∞[0,M; L²(Ω)]∩L²[0,M; H¹(Ω)],

采用类似文献[2]第4章的证明方法,当m→+∞,可得以下紧性框架:

‖U_～^m-U_～‖_{L¹(0,M; L¹(Ω))}→0,

|∫^M₀(B(U_～^m),φ_t)dt-∫^M₀(B(U_～),φ_t)dt|→0,

|∫^M₀b(U_～^m,φ)dt-∫^M₀b(U_～,φ)dt|→0,

|∫^M₀c(U_～^m,φ)dt-∫^M₀c(U_～,φ)dt|→0,

|∫^M₀e(U_～^m,U_～^m,φ)dt-∫^M₀e(U_～,U_～,φ)dt|→0,

其中,试验函数φ=(φ_vθ,φ_vλ,φ_T,φ_q)=(φ₁,φ₂,φ₃)∈C^∞(0,M; C^∞₀(Ω)),且有φ(M,·)=0,而U_～是系统(12)～(13)以U₀为初值的弱解.

本文研究了

参考文献[1]中考虑地形因素和随机外强迫作用的大尺度湿大气动力学方程组初边值问题的适定性问题. 该方程组有以下特点:1)将大气的运动过程视为一个随机过程; 2)大气上界气压可以取0; 3)考虑了大气的可压缩因素; 4)采用了较为复杂的边界条件.其次,在引入随机因素后,增加了诸如非线性平流项[(u+Z)·Δ](u+Z)和1/(p _～s)∫^ζ₀Δ·[p _～s(u^*+Z)]ds((u+Z))/(ζ)等的非线性程度,主要利用Hölder不等式、Minkowski不等式和插值不等式进行处理.最后,通过能量估计方法证明了方程组整体弱解的存在性,以及整体弱解的L¹稳定性和几乎处处稳定性. 未来将在此基础上,进一步证明该大气动力学方程组初边值问题整体强解及吸引子的存在唯一性等.