(School of Aerospace Engineering,Xiamen University,Xiamen 361102,China)
DOI: 10.6043/j.issn.0438-0479.202001028
备注
引言
自抗扰控制技术(active disturbance rejection control,ADRC)是韩京清[1]先生提出的一种非线性控制方法,由跟踪微分器、扩张状态观测器(extended state observer,ESO)和误差反馈控制器组成.ADRC继承了PID(proportional integral differential)“基于误差来消除误差”的思想,将被控对象中的各种扰动和不确定因素归结为总扰动,然后在控制器中进行补偿,从而将系统转换为积分串联的形式[2-3].它具有控制精度高、响应速度快、抗干扰能力强、对控制对象的模型依赖小等特点[4].为了减少调节参数、推广ADRC的应用,GAO[5]在ADRC的基础上提出了线性ADRC(LADRC),并将待整定的参数与控制器和观测器的带宽联系起来,从而将整定参数降低为3个,简化了系统结构,极大地促进了其在工程上的应用.
作为LADRC最重要的结构,线性ESO(LESO)承担着实时估计未知扰动的作用,从提出到现在,前人已经进行了大量细致的研究.Zheng等[6]分析了非线性时变系统LADRC的稳定性,并且证明当存在不确定性时,LESO跟踪误差是有界的.Xue等[7]分析了具有未知动力学和非连续扰动的不确定系统的自抗扰控制器性能.Zheng等[8]证明了具有不确定性n阶系统的LESO跟踪误差是有界的,并且带宽增加,误差单调递减.Huang等[9]采用自稳定区域(SSR)方法设计LESO,并分析了它的稳定性.Yang等[10]论证了LESO估计不确定性的能力,并进一步分析了LESO对正弦、方波、斜波等不同类型扰动的跟踪能力.LADRC已经广泛应用在工业电机控制[11]、电力控制系统[12]、军事武器[13]、航空航天[14]、下肢康复训练[15]等领域,其理论系统也更加完备.但目前研究主要关于LADRC的稳定性和LESO的收敛性及跟踪误差能力,未对LESO的暂态特性进行理论分析.文献[5,16]中使用“带宽”的思想,将极点统一配置到实轴上的一个具体位置,极大地减少了调节控制参数.该方法虽然也可以调节暂态性能,但是一定程度上缩小了LESO极点的取值范围,减弱了调节暂态性能的灵活性,与具有非线性结构的ESO相比,跟踪精度和响应速度受到制约,从而使暂态过程品质的提升受到限制.
为此,本文从暂态性能入手,沿用传统LESO“带宽法”的思想,通过加入两个调节因子灵活调节观测器的暂态性能和带宽,并根据实际情况平衡二者的关系,以达到最佳的跟踪效果.定量描述调节因子与暂态性能指标之间的关系,给出一般性结论,最大程度减少参数调节带来的困难.最后将改进化的LESO(improved LESO,ILESO)与传统的LESO做了仿真对比分析.
1 二阶系统的ADRC模型回顾
考虑单输入单输出的二阶系统
y ··=f(t,y(t),y ·(t))+b0u(t),(1)
其中,f(t,y(t),y ·(t))∈R是系统总扰动,u(t)∈R是控制输入,y(t)∈R是系统输出,b0∈R是控制输入系数.假设f(t,y(t),y ·(t))可微,将其扩展为一个新的状态量,将式(1)写为
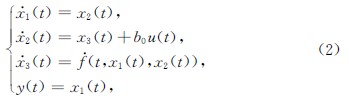
其中,x1=y,x2=y ·,x3=f(t,x1,x2).根据龙伯格提出的状态观测器理论[17],在确定性条件下对受控系统(2)的状态进行重构,对应的LESO方程形式如下:
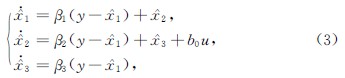
其中,x ∧1、x ∧2、x ∧3是LESO的状态变量,参数β1、β2和β3共同构成观测器增益矩阵[β1,β2,β3]T.通过适当选取参数β1、β2和β3,可实现观测器对系统(2)中各个状态变量的跟踪.显然,观测器(3)对应的特征方程如下:
LLESO(s)=s3+β1s2+β2s+β3.(4)
文献[16]通过将观测器的3个极点统一配置到左半实轴-ωo处,来确定观测器增益矩阵.令
LLESO(s)=(s+ωo)3,(5)
即β1=3ωo,β2=3ω2o,β3=ω3o,得到观测器增益矩阵:
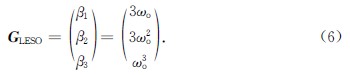
其中ωo为LESO的带宽.在得到系统总扰动f(t,x1,x2)的估计x ∧3之后,可通过设计如下控制输入量u,进而完成对系统(1)的镇定或跟踪控制目标,
u=1/(b0)(u0-x ∧3),(7)
其中u0是虚拟控制量.将控制量u代入系统(1)可得
y ··=u0,(8)
从而实现非线性系统补偿之后的线性化.系统(1)转化为积分串联形式,进一步选取
u0=-β01(x ∧1-v)-β02x ∧2,(9)
其中,v是设定被跟踪的信号值,β01和β02共同构成控制器状态反馈矩阵[β01,β02].再令η1=x ∧1-v,η2=x ∧2,综合观测器的性质可得
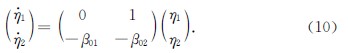
适当选取参数β01和β02,可以保证系统输出渐近跟踪输入信号.显然,控制器(6)的特征方程如下:
C(s)=s2+β02s+β01.(11)
文献[16]通过将控制器的2个极点配置到左半实轴-ωc处,来确定控制器状态反馈系数.即令
C(s)=(s+ωc)2,(12)
得到状态反馈系数为
β01=ω2c,β02=2ωc,(13)
再次削减了调节参数的数量,其中ωc为控制器的带宽.
综上所述,在不考虑跟踪微分器时,式(3)、(7)和(9)共同构成了LADRC[16].
2 改进型线性扩张状态观测器
2.1 ILESO的形式文献[5,16]中的LESO将极点统一配置到实轴上的一个具体位置,虽然也可以调节系统的暂态性能,但是减弱了调节暂态性能的灵活性,一定程度上制约了跟踪精度和响应速度,必然使暂态过程品质的提升受到限制.ILESO在此基础上额外给两个参数β2和β3各乘上一个调节因子,便可以灵活改变极点的位置,从而改进观测器的暂态性能.
对比传统LESO的表达式(3),给出三阶ILESO的方程如下:
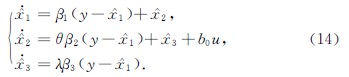
根据式(5),ILESO的增益矩阵更新为
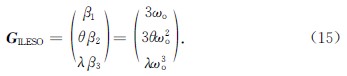
对式(14)进行拉氏变换可得
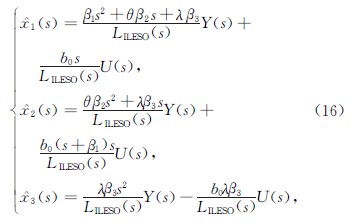
其中LILESO(s)是ILESO的特征方程,具体为
LILESO(s)=s3+β1s2+θβ2s+λβ3.(17)
2.2 配置ILESO的主导极点对系统式(1)进行拉氏变换:
s2Y(s)=F(s)+b0U(s).(18)
将式(18)代入式(16)中的x ∧3(s)中可得
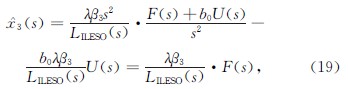
则系统总扰动F(s)到它的观测量x ∧3(s)的传递函数为
Ψ(s)=(x ∧3(s))/(F(s))=(λβ3)/(LILESO(s))=
(λβ3)/(s3+β1s2+θβ2s+λβ3).(20)
在实际情况中,一般使调节因子θ满足如下条件:
θ>(27)/(25).(21)
根据一元三次方程的盛金判别法[18]可以证明,当满足式(21)时,Ψ(s)的特征方程L*(s)=0有1个实根和2个共轭复根.在满足稳定性的条件下,它们均位于s平面左半部分.假设实根为-ra,共轭复根为-a+bi、-a-bi,其中a、b、r均为正数,i为虚数单位.因此传递函数式(20)可以重写为如下形式:
Ψ(s)=(λβ3)·{[s-(-ra)][s-(-a+bi)]
[s-(-a-bi)]}-1.(22)
根据一元三次方程根与系数的关系以及LESO增益矩阵式(6)可得
(2+r)a=β1=3ωo,(23)
(2r+1)a2+b2=θβ2=θ3ω2o,(24)
ra(a2+b2)=λβ3=λω3o.(25)
根据式(23)~(25)可以进一步推出如下关系:
3a2-2β1a+θβ2=b2,(26)
8a3-8a2β1+2a(β21+θβ2)+λβ3-θβ1β2=0,(27)
rθβ1β2(2+r)2-2r2β13-λβ3(2+r)3=0,(28)
(β1-2a)(a2+b2)-λβ3=0.(29)
为了简化分析和加快系统响应速度,利用“主导极点”的思想,令实数极点远离虚轴,使参数r满足如下条件:
r>3.(30)
将式(28)变换为如下形式:
r(θβ1β2-λβ3)-2λβ3=(2r2β13)/((2+r)2).(31)
在式(30)的约束下,由式(31)可以推导出此时调节因子θ和λ必须满足如下关系:
λ>(27θ)/5-(486)/(125).(32)
根据高阶系统的时域分析法[19],舍掉非主导极点部分,式(22)中传递函数Ψ(s)可以近似为二阶系统,重新配置增益,将其变换为如下形式:
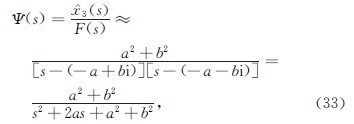
系统阻尼比
ξ=a/((a2+b2)1/2).(34)
显然,此时ψ(s)为二阶欠阻尼系统.
2.3 调节因子取值范围根据古典控制理论中的劳斯判据,列出式(17)LILESO(s)的劳斯列表(表1).
为了保证系统稳定性,调节因子需满足下列条件:
0<λ<(β1β2)/(β3)θ.(35)
综合增益矩阵式(6)和2.2中的式(21)、(30)和(32),可得ILESO调节因子θ和λ的取值范围如下:
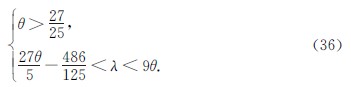
值得注意的是,引入“主导极点”的思想是为了便于简化分析.在工程中可以放宽式(30)和(32)的约束要求,根据控制精度要求和抑制高频扰动的带宽要求,按照实时仿真的结果,灵活改变调节因子的取值,以达到最佳控制效果.
在工程实际操作中,可以先设置θ=1,λ=1,大致调节(粗调)ωo,使观测器性能达到一个相对合理的程度,然后根据式(36)的调节因子取值范围适当微调(精细调节)θ和λ的取值,从而达到进一步改进观测器性能的目的.
3 ILESO的跟踪误差
先考虑传统LESO的跟踪误差,文献[5]中已经证明传统LESO是BIBO(bounded-input bounded-output)稳定的.令观测器跟踪误差ei=xi-x ∧i,(i=1,2,3),eLESO=(e1,e2,e3)T,综合式(2)和(3)可得
e ·LESO=AeLESO-G(y-y ∧)+Ef ·=
(A-GC)eLESO+Ef ·.(37)
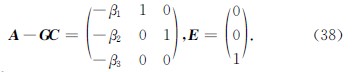
令A ~=A-GC,w=f ·,误差初值为eLESO(0),扰动的导数有界|w|≤δ,那么误差方程(37)在时域上的解为
eLESO(t)=exp(A ~t)eLESO(0)+∫t0exp(A ~(t-τ))×
E×w(τ)dτ.(39)
假设A~负定,那么等式右边第一项零输入响应很快衰减为0,稳态误差满足
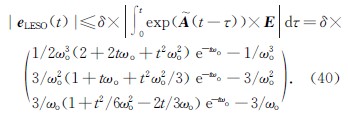
进一步计算可得LESO的稳态误差上界
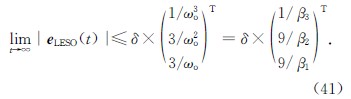
实际应用中,考虑慢时变系统,即δ=0,通过适当选取β1、β2和β3,可实现观测器对系统中各个状态变量的跟踪,即limt→∞|x ∧1-x1|=0,limt→∞|x ∧2-x2|=0,limt→∞|x ∧3-x3|=0.
显然对于ILESO,它的稳态误差也是有界的,在传统LESO的基础上,其形式如下:
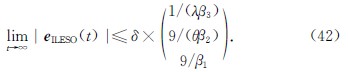
因此可得结论:当线性时不变系统含有扰动,且扰动的导数有上界δ,那么ILESO的跟踪误差也有界,且远小于δ.进一步增大观测器增益系数,可以降低跟踪误差,即达到一种实用稳定.
对于ILESO,因为λ>1,θ>1,在相同条件下,其跟踪误差相比于传统LESO更小.
4 ILESO的时域暂态性能
4.1 调节时间调节时间是指响应到达并保持在终值±5%或±2% 误差内所需的最短时间[19],根据欠阻尼二阶系统的时域性能指标的结论,选取误差带Δ=0.02,根据式(33),调节时间可表示为
ts=4.4/a.(43)
在式(27)中,参数a是调节因子θ和λ的隐函数,分别对θ和λ求导可得
a'(θ)=1/2·(β2(β1-2a))/(12a2-8β1a+β21+θβ2)=
(β2)/2·((β1-2a))/(12(a-(β1)/3)2+θβ2-(β21)/3),(44)
a'(λ)=-(λ3)/2·1/(12a2-8β1a+β21+θβ2)=
-(λ3)/2·1/(12(a-(β1)/3)2+θβ2-(β21)/3).(45)
综合式(6)、(21)和(23)可知,a'(θ)>0,a'(λ)<0恒成立,因此参数a与θ正相关,与λ负相关.
综上所述,增大调节因子θ或者减小λ,都会使调节时间减少,从而加快系统响应速度.
4.2 超调量根据欠阻尼二阶系统的时域性能指标的结论[19],超调量可以表示为:
σ%=e-(aπ)/b×100%.(46)
下面对超调量作进一步的讨论.
(i)调节因子λ不变,调节θ.
联立式(23)和(30),可得参数a的取值范围如下:
0<a<(β1)/5.(47)
将式(44)化成如下形式:
a'(θ)=(β2)/2·1/(3(β1-2a)+(θβ2)/(β1-2a)-2β1)=
(β2)/2·1/(3m+(θβ2)/m-2β1),(48)
其中m=β1-2a,且3m+θβ2/m-2β1>0.根据式(47)可知
(3β1)/5<m<β1.(49)
在式(26)中,参数b是调节因子θ的隐函数,对θ求导可得
b'(θ)=(β2-2a'(θ)·(β1-3a))/(2b),(50)
将式(48)代入式(50)中可得
b'(θ)=(3β2)/(4b)·1/(m(3m+(θβ2)/m-2β1))·
((2θβ2)/3-m(β1-m).(51)
综合式(6)和(49)可知,当满足式(21)的条件时,重写为
θ>(27)/(25),
可以保证b'(θ)>0恒成立.
a/b同样是调节因子θ的隐函数,对θ求导可得
((a(θ))/(b(θ)))'=1/(b2)[a'(θ)b(θ)-b'(θ)a(θ)].(52)
将式(48)和(50)代入式(52)中,联立式(26)可得
((a(θ))/(b(θ)))'=((θβ2-aβ1))/(2b3)(2a'(θ)-(aβ2)/(θβ2-aβ1))=
(β2(θβ2-aβ1))/(2b3)(h(θ))/((3m+(θβ2)/m-2β1)((2θβ2)/(β1-m)-β1)),(53)
其中
h(θ)=β1-3m+(2θβ2)/(β1-m)-(θβ2)/m=(3m-β1)/(m(β1-m))·
(θβ2-m(β1-m)).(54)
综合式(49)可知,当θ>1时
((a(θ))/(b(θ)))'>0,(55)
h(θ)>0恒成立,所以a/b和调节因子θ正相关.
(ii)调节因子θ不变,调节λ.
综合分析式(26),考虑到式(47),易知参数a和b负相关,即a/b和调节因子λ负相关.
综上所述,增大调节因子θ或者减小λ,都会使超调量σ%减少.
4.3 峰值时间峰值时间是指阶跃响应超过终值,到达第一个峰值所需的最短时间[19].可以表示为
tp=(π)/b.(56)
根据前面对参数a和b的分析可知,增大调节因子θ或者增大λ,都可以使峰值时间减小.
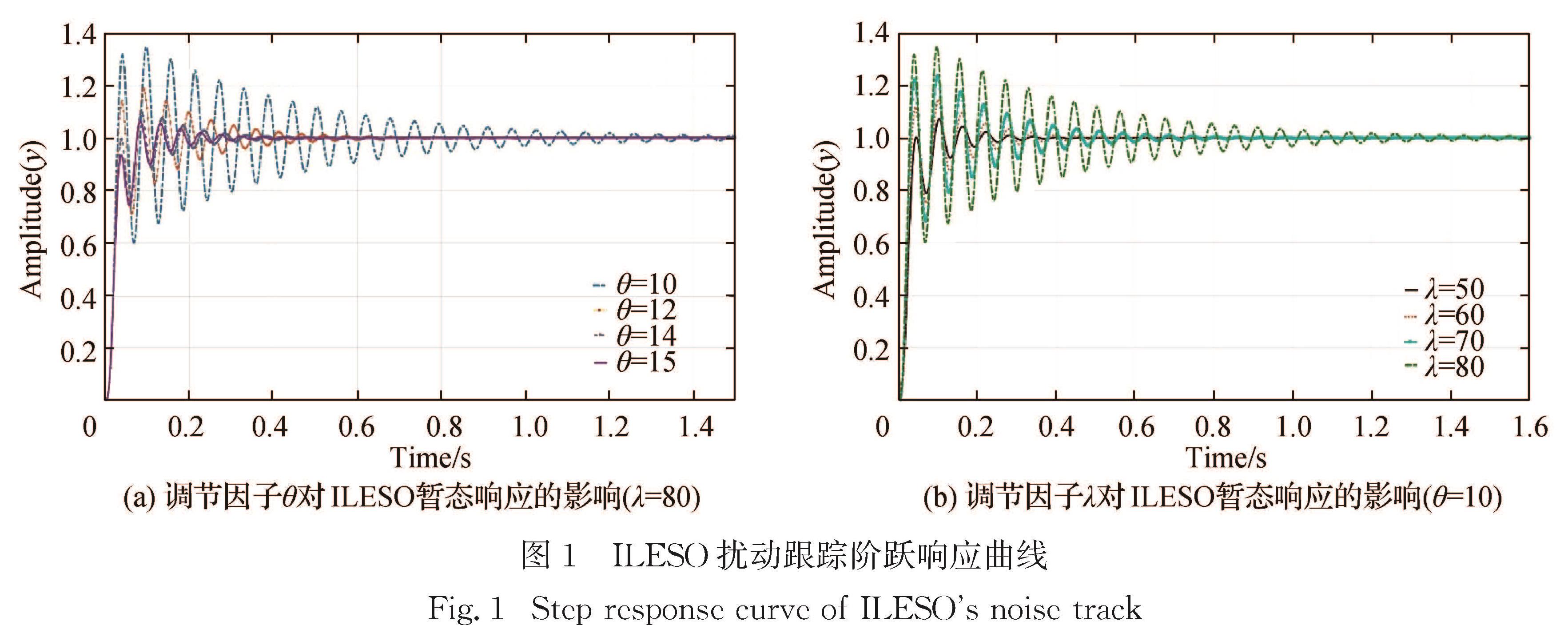
为了验证上述理论分析,设定输入v为单位阶跃信号,ωc=5 rad/s,ωo=20 rad/s,设置调节因子λ=80,θ分别取值为10,12,14,15,ILESO状态变量x ∧3的阶跃响应对比曲线如图1(a)所示,图中横坐标是仿真时刻,纵坐标是信号幅值.
其他条件不变,设置调节因子θ=10,λ分别取值为50,60,70,80,ILESO的状态变量x ∧3的阶跃响应如图1(b)所示.
图1(a)仿真结果说明,增大调节因子θ可以减少调节时间、超调量和峰值时间; 图1(b)说明,增大调节因子λ会增大调节时间和超调量,但峰值时间减小.该结论与上述理论分析吻合.
值得注意的是,如一直增大θ,则会破坏式(30)和(32)的约束条件,且超调量会消失,调节时间会转而增加,响应会变缓慢,因此调节因子θ不能无限增加.
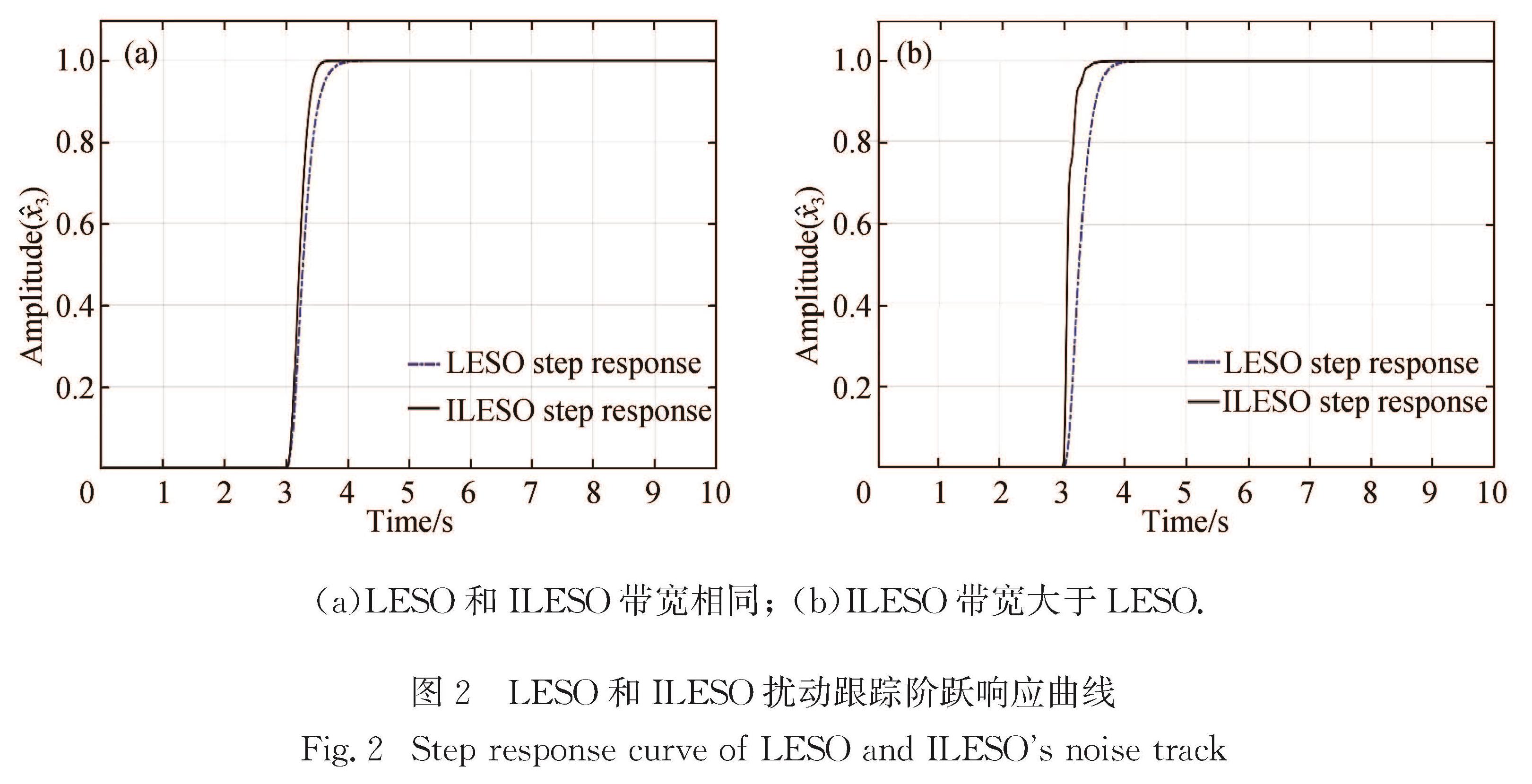
设定ωc=5 rad/s,ωo=10 rad/s,θ=1.2,λ=1.6,此时ILESO带宽ωb=11.17 rad/s≈ωo.传统LESO和ILESO状态变量x ∧3的阶跃响应对比曲线如图2(a)所示,图中横坐标是仿真时刻,纵坐标是信号幅值.
若放开对ILESO带宽的限制,设定ωc=5 rad/s,ωo=10 rad/s,θ=8.4,λ=24,此时ILESO带宽ωb=72.56 rad/s>ωo.传统LESO和ILESO状态变量x ∧3的阶跃响应对比曲线如图2(b)所示.
(a)LESO和ILESO带宽相同;(b)ILESO带宽大于LESO.
从图2(a)中可以看出,在带宽近似相同,即观测器对扰动抑制能力不变的情况下,依靠调节两个因子可以使得ILESO的峰值时间比LESO更短,响应速度更快.从图2(b)中可以看出,增大带宽可以加快系统响应速度,该结论与已有经验吻合.
5 ILESO的带宽
将式(33)中的Ψ(s)近似看作ILESO扰动跟踪的闭环传递函数.根据闭环系统的频域性能指标[19],设ILESO的观测带宽为ωb,可以列出如下方程:
|Ψ(iωb)|=|(a2+b2)/((iωb)2+2a(iωb)+(a2+b2))|=
(21/2)/2|Ψ(0)|=(21/2)/2,(57)
化简可得
ω4b-2(b2-a2)ω2b-(a2+b2)2=0.(58)
解式(58)中关于ω2b的二次方程可得
ω2b=b2-a2+(2(a4+b4))1/2.(59)
综合4.1~4.3节中的结论可知,增大调节因子θ或者增大λ,都会使观测带宽ωb增加; 并且ILESO的观测带宽ωb可以由式(23)~(25)和式(59)定量计算得到.
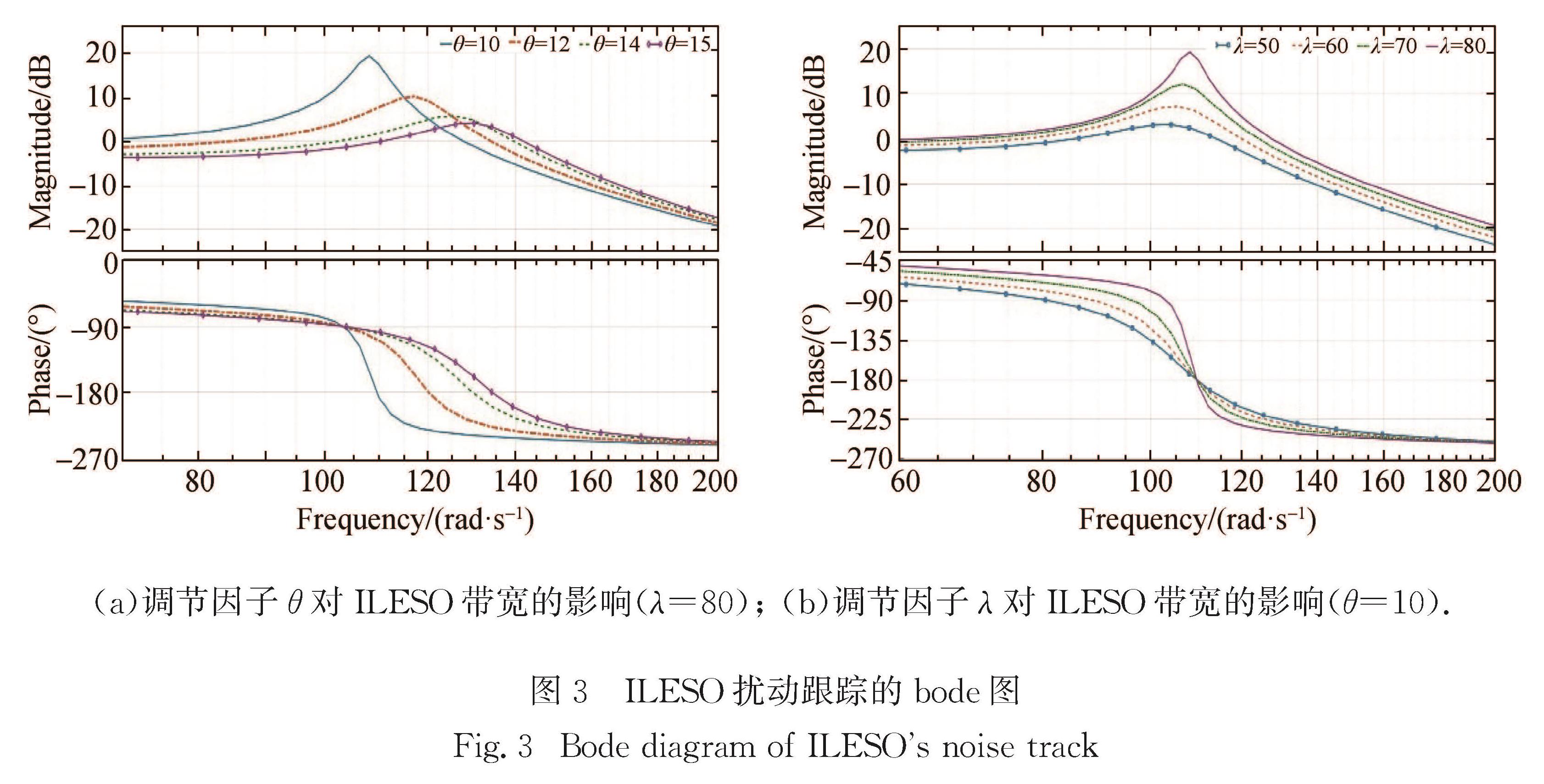
为了验证上述分析,设定ωc=5 rad/s,ωo=20 rad/s,调节因子λ=80,θ分别取值为10,12,14,15,根据2.2节中式(20)给出的ILESO扰动跟踪的闭环传递函数,绘制bode图对比曲线如图3(a)所示,bode图中横坐标是扰动频率,纵坐标分别是信号幅值和相位.
其他条件不变,设定调节因子θ=10,λ分别取值为50,60,70,80,ILESO扰动跟踪的闭环传递函数的bode图对比曲线如图3(b)所示.
从图3(a)可以看出,增大调节因子θ,ILESO的观测带宽ωb增加; 从图3(b)可以看出,增大调节因子λ,ILESO的观测带宽ωb增加.该结论验证了上述理论分析的正确性.
6 ADRC整体仿真
6.1 传统LESO综合式(1)、(3)、(7)和(9),搭建LADRC的Simulink仿真框图,并编写相应Matlab程序.将两个调节因子θ和λ分别置为1,此时ILESO等同于传统LESO.设定输入v为单位阶跃信号,LESO的带宽ωo为20 rad/s,控制器带宽ωc为5 rad/s,并使系统(1)控制输入系数b0=1.
假设总扰动包含的正弦波频率为18(rad/s),矩形波周期为π(s),斜坡信号斜率为0.5,即

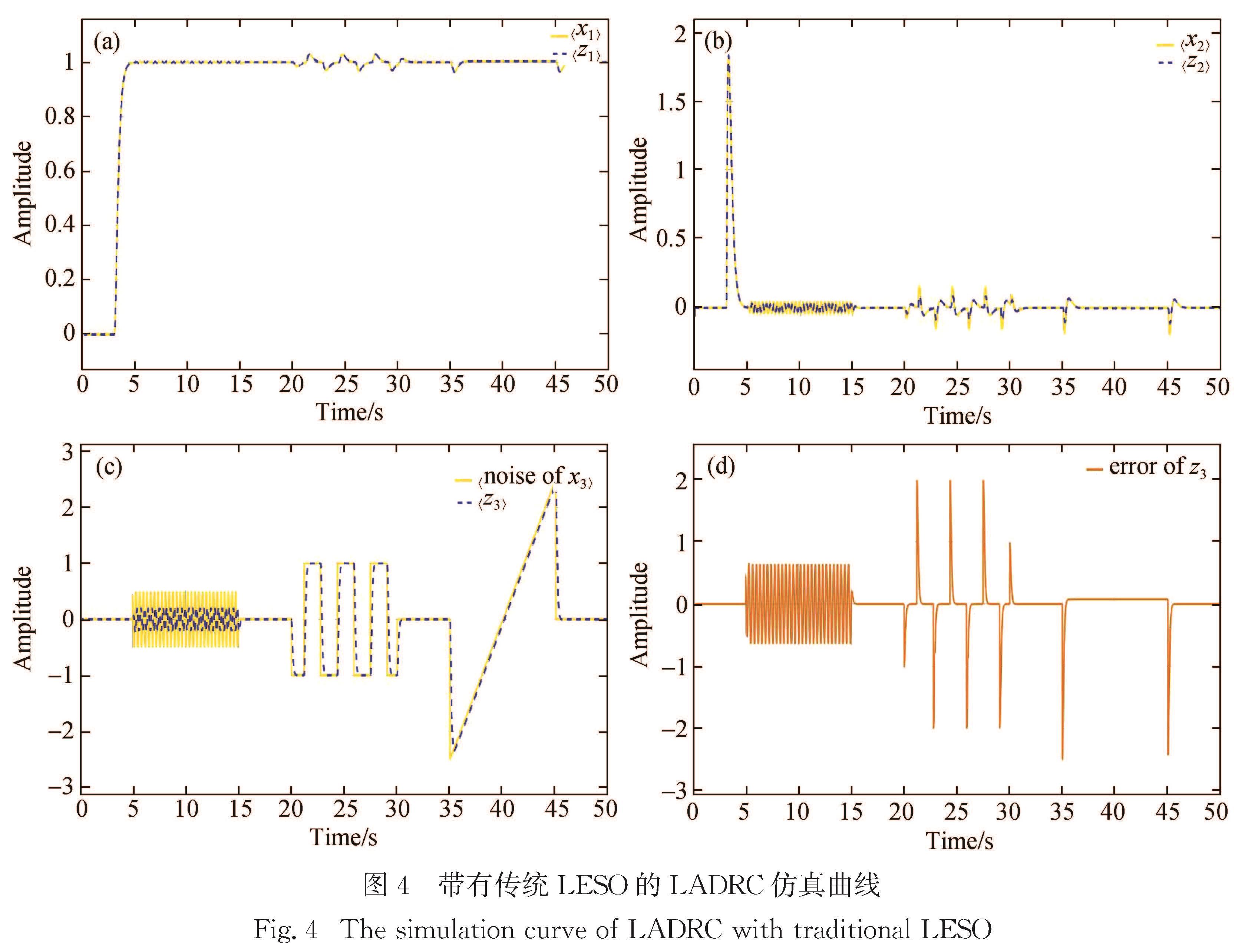
仿真结果如图4所示,图中横坐标是仿真时刻,纵坐标是信号幅值,测得此时矩形波的调节时间为ts≈0.45 s.
图4(a)~(c)依次为系统状态变量x1、x2、x3和LESO观测量x ∧1(z1)、x ∧2(z2)、x ∧3(z3)的对比曲线,以及LESO扰动跟踪x ∧3(z3)的误差曲线(图4(d)).可以看出LESO跟踪误差比较大,且对矩形波的响应速度较慢.
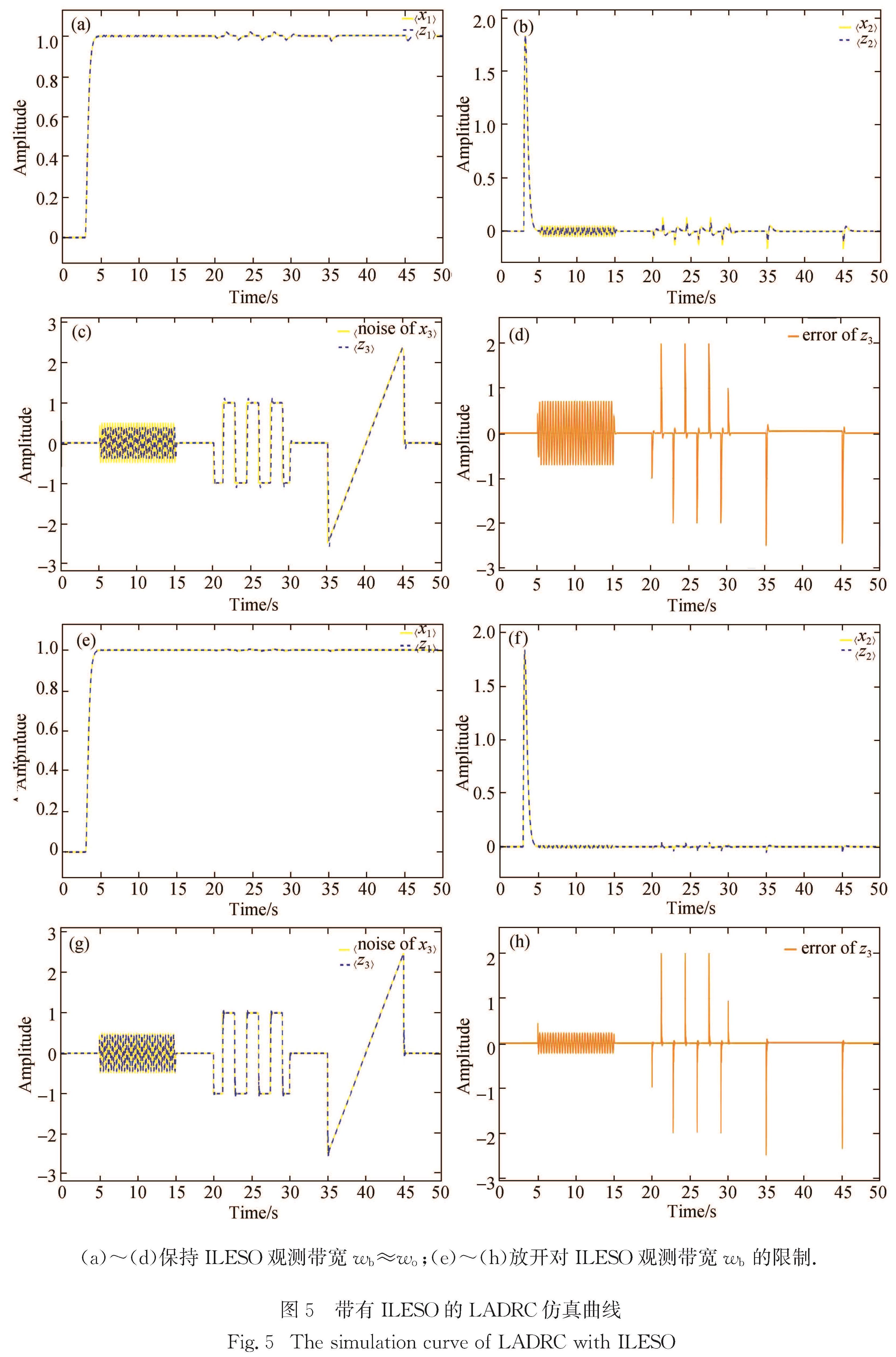
6.2 改进型LESO(ILESO)重新设置调节因子θ=1.08,λ=1.785,保持 3.1节中其余仿真参数和仿真条件不变.此时ILESO的带宽ωb=22.6 rad/s≈ωo,测得调节时间ts<0.35 s,超调量σ%<12%,仿真结果如图5(a)~(d).
(a)~(d)保持ILESO观测带宽wb≈wo;(e)~(h)放开对ILESO观测带宽wb的限制.
重新设置调节因子θ=15.5,λ=80,保持3.1节中其余仿真参数和仿真条件不变,此时ILESO观测带宽ωb≈205 rad/s,仿真结果如图5(e)~(h).
从图5(a)~(d)可以看出,在与传统LESO的带宽ωo基本保持不变的情况下,正弦波、矩形波、斜坡的暂态响应速度已经明显加快.从图5(e)~(h)可以看出,当放开对带宽的限制时,灵活改变两个调节因子θ和λ的值,矩形波的调节时间和超调量几乎可以忽略不计,正弦信号跟踪误差也大幅减小.
对比图4和图5可以看出,ILESO只需通过两个调节因子的搭配就可以优化观测器的调节时间和超调量,灵活调节暂态响应的速度和跟踪误差.
7 结 论
针对二阶系统ADRC的LESO暂态跟踪性能的不足和带宽之间的矛盾,提出了一种ILESO.在传统“带宽法”配置极点的基础上,在观测器方程中增加两个调节因子,从而可以根据外部噪声的频率和内部扰动的特征,灵活配置极点位置,增进了观测器的暂态性能.扰动观测带宽的大小可以根据实际情况灵活调节,增强了对噪声的抑制能力.通过理论分析,得到两个调节因子与系统暂态性能、带宽之间的定性关系.通过实验仿真对比,证明了该方法的优越性,为实际的工程控制应用提供了一种新方法.本文中基于“带宽法”提供了时域分析的一种方法,另一种思路是直接通过“主导极点”分析给出暂态性能和观测器主导极点参数之间的关系,是值得将来进一步考虑的问题.
- [1] 韩京清.自抗扰控制器及其应用[J].控制与决策,1998,13(1):19-23.
- [2] 邵星灵,王宏伦.线性扩张状态观测器及其高阶形式的性能分析[J].控制与决策,2015,30(5):815-822.
- [3] 韩京清.自抗扰控制技术——估计补偿不确定因素的控制技术[M].北京:国防工业出版社,2008.
- [4] 袁东,马晓军,曾庆含,等.二阶系统线性自抗扰控制器频带特性与参数配置研究[J].控制理论与应用,2013,30(12):1630-1640.
- [5] GAO Z Q.Scaling and bandwidth-parameterization based controller tuning[C]∥American Control Conference.Denver:IEEE,2003:4989-4996.
- [6] ZHENG Q,GAO L,GAO Z Q.On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics[C]∥IEEE Conference on Decision and Control. New Orleans:IEEE,2007:3501-3506.
- [7] XUE W C,HUANG Y.On performance analysis of ADRC for nonlinear uncertain systems with unknown dynamics and discontinuous disturbances[C]∥Chinese Control Conference.Piscataway:IEEE,2013:1102-1107.
- [8] ZHENG Q,GAO L Q,GAO Z Q.On validation of extended state observer through analysis and experimentation[J].Journal of Dynamic Systems,Measurement,and Control,2012,134(2):024505.
- [9] HUANG Y,HAN J Q.Analysis and design for the second order nonlinear continuous extended states observer[J].Chinese Science Bulletin,2000,45(21):1938-1944.
- [10] YANG X,HUANG Y.Capabilities of extended state observer for estimating uncertainties[C]∥American Control Conference.Piscataway:IEEE,2009:3700-3705.
- [11] 程剑彬,孙宗海.基于线性自抗扰的开关磁阻电机调速控制研究[J].计算机测量与控制,2018,26(11):108-111.
- [12] 杨林,曾江,黄仲龙.线性自抗扰技术在LCL逆变器并网电流控制及有源阻尼中的应用[J].电网技术,2019,43(4):1378-1386.
- [13] 陈水忠,刘敏.基于自抗扰的机载激光武器跟踪控制系统设计[J].电光与控制,2017,24(7):85-89.
- [14] 朴敏楠,孙明玮,黄建,等.基于自抗扰的高超声速飞行器姿态鲁棒控制[J].控制工程,2019,26(9):1627-1635.
- [15] 赵兴景,朱杰,罗翔.自抗扰技术在下肢康复训练器中的应用[J].东南大学学报(自然科学版),2019,49(6):1026-1032.
- [16] 朱斌.自抗扰控制入门[M].北京:北京航空航天大学出版社,2017:20-45.
- [17] 王宏华,王时胜.现代控制理论[M].北京:电子工业出版社,2006:226-231.
- [18] 范盛金.一元三次方程的新求根公式与新判别法[J].海南师范学院学报,1989,2(2):91-98.
- [19] 胡寿松.自动控制原理基础教程[M].北京:科学出版社,2013:98-191.