基金项目:国家自然科学基金(61671399); 中央高校基本业务费专项(20720190012)
通信作者:lswang@xmu.edu.cn
(School of Informatics,Xiamen University,Xiamen 361005,China)
DOI: 10.6043/j.issn.0438-0479.202003042
研究新型冠状病毒肺炎(COVID-19)传播方式规律及趋势有助于有效遏制其蔓延.介绍了一些常用的传染病预测模型,提出了Logistic_SEIR模型,既克服了Logistic模型不能预测现有确诊人数的缺点又克服了SEIR模型调参太多的缺点,并通过实验证明了所提出模型的实现和预测的优越性.同时进一步研究了Logistic_SEIR模型需要调试的参数取不同的初始值对预测结果的影响,并通过加权误差来量化分析预测效果.最后指出未来进一步的研究方向.
To study the law and trend of coronavirus disease 2019(COVID-19)transmission mode is helpful for effectively curbing its spread.In this article,we first introduce some commonly used prediction models of infectious diseases,and then introduce the Logistic_SEIR model.This model not only overcomes shortcomings of the Logistic model that cannot predict the number of confirmed patients,but also overcomes those of the SEIR model in which plenty of parameters exist.In experiments,we prove the superiority of the realization and prediction of the model proposed in our study.At the same time,we further study the influence of different initial values of the parameters that need to be debugged in the Logistic_SEIR model on the prediction results,and quantifies the prediction effect through the weighted error.Finally,in the summary,we point out the future research directions.
新型冠状病毒(SARS-CoV-2)以前从未在人体中发现[1-3].人感染了冠状病毒后常见体征有呼吸道症状、气促、咳嗽、发热和呼吸困难等.在较严重病例中,还可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.到目前为止仍没有特异性方法来治疗新型冠状病毒肺炎(COVID-19)[3].
COVID-19疫情还在全球蔓延,了解其传播途径及规律尤为重要.飞沫传播和接触传播是COVID-19的主要传播途径,气溶胶和粪-口传播也是可能的传播途径[4-5].
COVID-19的传播规律可结合近年来其他一些传染病常用的预测模型来研究.依据2003年我国香港地区与新加坡的SARS疫情统计数据,已有研究[6-8]建立了动态数学模型.Gong等[9]为了研究“早发现、早隔离、早治疗”措施,对于控制SARS疾病传播的重要性,建立了系统动力学模型.他们进一步设计了SARS 时空传播动力学模型及与SARS模型关联非常密切的智能体知识库和决策引擎, 实现了一系列的规则对智能体的行进引导[10].
起初用于模拟人口增长的Logistic模型[11]也常被用于模拟传染病人数增长规律,其函数表达式为:
P(t)=KP0ert/[K+P0(ert-1)].(1)
其中:P0为人口初始值,表示传染病模型中的初始感染人数; K为环境容量,表示传染病模型中的最大累积感染人数; r为衡量曲线变化快慢,表示传染病模型中的疾病传染率; t为时间,P(t)为随时间变化的人口数量,表示传染病模型中的随时间变化的累计感染人数.因为该模型是单调递增的,所以只能预测累计感染人数,无法预测现有确诊人数.
常用预测现有确诊人数的模型有SI(susceptible-infectious)模型[12]、SIS(susceptible-infectious-susceptible)模型[13]、SIR(susceptible-infectious-recovered)模型[14-15]、SEIR(susceptible-exposed-infectious-recovered)模型[16-17]等.这些模型的复杂性依次增加,复杂模型更符合传染病真实传播规律.最复杂的SEIR模型的示意图如图1所示.
SEIR模型把人群划分成4类:易感者(susceptible),即没有抗体的健康者,用S表示易感人数; 潜伏者(exposed),用E表示潜伏者人数; 感染者(infected)即患者,用I表示患者人数; 康复人群(recovered),用R表示康复人数(这里的康复者包括死亡人群).总人数N=S+E+I+R.健康人的比例为S/N.
该模型比其他3种模型更符合COVID-19的发病形式,SEIR模型的微分方程为:
dS/dt=-rβIS/N,(2)
dE/dt=rβIS/N-αE,(3)
dI/dt=αE-γI,(4)
dR/dt=γI,(5)
其中,r代表一个感染者遇到的人数,β为健康人变为潜伏者的感染率概率,γ为患者恢复健康的康复率,α代表潜伏者转阳成为患者的概率.SEIR模型是这4个模型中最复杂的,包含其他3种,也最符合实际传染病的传播规律,故下文提到这4个模型用SEIR代表.
上述这些模型中Logistic模型只能预测累计感染人数,不能预测现有确诊人数.SEIR模型可以模拟传染病传播过程中各类人群数量的变化,但如果预测COVID-19每天的现有确诊人数I,则需要对刚开始的健康者人数S、潜伏者人数E、感染者人数I、康复者人数R、健康者变为潜伏者的感染率β、潜伏者转阳成为感染者的传染率α、传染者变为康复者的康复率γ共7个参数进行调参,这个过程非常困难繁琐,还需要额外的先验知识.本文提出的Logistic与SEIR结合模型(简称Logistic_SEIR模型)可以解决这些问题,能大大减少调参的数量,只需对3个参数进行简单调参,就可以取到很好的预测效果.
Logistic_SEIR模型的思路是:Logistic模型里的参数初始感染人数P0、最终累计感染人数K和传染速率r,在训练集里训练后可以自动获取,可用Logistic模型里的r初始化SEIR模型里的β,用Logistic模型里的P0初始化SEIR模型里的初始感染者人数I和潜伏人数E(或者用真实数据里第一天的感染者人数初始化I和E).康复者人数R用真实数据里第一天康复者人数加上死亡者人数初始化(或者初始化为0).因为在一定范围内初始时的健康者人数近似于最终累计的感染人数(比最终累计感染人数多),所以可以用Logistic模型里的K乘以一个大于1的系数初始化SEIR模型里健康者人数S.潜伏者发病变为感染者的传染率α、传染者变为康复者的康复率γ可以比较容易地调试,且使预测效果很好.
Logistic_SEIR模型实现的流程及算法步骤:
1)把数据集按9:1划分为训练集和测试集.
2)根据式(1)(Logistic公式)定义Logistic函数:
logistic_function(t,K,P0,r):
return KP0 ert /[K+P0(ert-1)]
根据式(2)~(5)(SEIR模型微分方程)定义SEIR模型函数:
diff_SEIR(V=[S,E,I,R]):
Y[0]=-β×V[0]×V[2]
Y[1]=β×V[0]×V[2]-V[1]×α
Y[2]=α× V[1]-γ×V[2]
Y[3]=γ×V[2]
return Y
3)利用scipy模块里的curve_fit方法采用非线性最小二乘法在训练集上拟合Logistic函数,得到Logistic模型里的参数:初始感染人数P0,最终累计感染人数K,传染速率r.该过程利用scipy里的curve_fit只需一行代码就可实现.
4)利用步骤3)得到的参数部分初始化SEIR模型参数,并初始化剩余参数.
5)通过spi.odeint求解SEIR模型的微分方程,得出现有确诊人数的预测值.该过程利用scipy.integrate里的odeint一行代码就可实现.
本文提出的Logistic_SEIR模型大大降低了单独SEIR模型调参的数量和难度,由7个降为3个,并且需要调参的参数可以在一定范围内调试,比较容易地取得不错的预测效果.
实验数据来源于github网站(https:∥github.com/zwdnet/2019-nCov-SIRmodel/blob/master/data.
csv.),该网站数据是从国家卫生健康委员会网站整理成csv格式得到的.数据日期从2020年1月10日开始,因为从1月21日开始统计全国感染人数,所以本文数据集为从2020年1月21日至2月29日共40天全国COVID-19的官方数据.数据包括日期(date)、感染者、疑似者、死亡、治愈等.计算现有确诊人数项,现有确诊人数等于感染者人数减去死亡人数减去治愈人数.训练和预测时把日期作为自变量x,现有确诊人数作为因变量y.为了方便,把日期作个变换,把第一次出现感染者的日期即2020年1月21日记为0,往后日期依次顺延1,2,3,….为了验证训练效果,把数据按9:1的比例分为训练集(2020年1月21日至2月25日,共36天)和测试集(2020年2月26—29日,共4天).为了进一步说明本文模型的预测效果,把2020年3月1—21日,共21天的数据作为额外测试集.
试验环境:CPU环境,3.6.9版本的python,1.4.1版本的scipy,3.1.2版本的matplotlib,0.21.3版本的sklearn及其他一些必要的库.
Logistic_SEIR模型采用的初始化参数是Logistic模型在训练集上得出的参数.实验分两部分:1)Logistic_SEIR模型预测现有确诊人数; 2)分析各个参数对Logistic_SEIR模型预测效果的影响.
根据Logistic公式定义Logistic函数,利用scipy里的curve_fit方法在训练集上利用非线性最小二乘法拟合Logistic函数,得到初始感染人数P0、最终累计感染人数K、传染速率r这3个参数的值,用训练得到的参数K、P0、r来初始化SEIR模型的一些参数.在SEIR模型中,S0代表初始健康者人数,Logistic模型里的参数K代表环境容量,考虑到初始的健康人数比最终累计的感染人数多,本文用K乘以一个大于1的系数来对S0进行初始化.因为系数不会很大,所以在1和2之间调试,间隔先为0.1,对预测结果进行比较,接着在预测效果最好的系数值附近加0.05,减0.05,比较这3个系数哪个预测效果好.最终得出K×1.35在训练集和测试集上预测效果最好,故本文S0=K×1.35.SEIR模型中E0代表初始潜伏者人数,用Logistic模型里的参数P0初始化,SEIR模型中I0用数据集中第一天的感染人数初始化,SEIR模型中R0用真实数据第一天的死亡人数与康复人数的和初始化.由于潜伏者也存在传染的能力,所以把传染率分为潜伏者的传染率β2和感染者的传染率β.本文把两个传染率β2和β乘以r除以N的值用Logistic模型参数里的r/N初始化,潜伏者变为感染者的传染率α用1/4初始化(潜伏者转阳的概率α较大,故本文对α进行1~8的倒数赋值,通过比较得出α=1/4拟合效果最好),康复率γ用1/18初始化(治愈率随疫情的变化不断在变化,故我们通过对γ赋不同值的比较,在1/20~1/2之间比较得出γ=1/18在训练集上拟合,测试集上预测效果最好.随着疫情发展治愈率在增加,故进行更长远预测需要进一步提高康复率).为说明本文模型的效果,用单独的SEIR模型作对照实验.单独的SEIR模型参数的初始化要根据额外的数据进行设定,且难度较大.根据现有数据预估累计感染人数峰值在8万多人,故本文把单独SEIR模型的初始健康人数S0初始化为85 000,潜伏者E0初始化为0,感染者I0初始化为第一天实际的感染人数,康复者R0初始化为第一天治愈人数与死亡人数的和.传染率β和β2根据SARS的传染率设置,即一个人传染2~3个人,故β和β2初始化为3/85 000,潜伏者变为感染者的感染率α初始化为2/3,康复率γ根据官方给出COVID-19的治愈率在50%左右,初始化为0.5.对比结果如图2所示.
图2 Logistic_SEIR模型预测现有确诊人数
Fig.2 Logistic_SEIR model prediction of the number of existing infected population
可见单独的SEIR模型预测效果很不理想,而且想要取得好的预测效果,需要多次调试7个参数,这是一项复杂艰巨的工作.为了更加清楚地了解模型的预测效果,用均方根误差(RMSE)进行量化分析,具体如下:
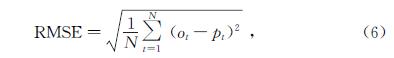
其中,pt和ot代表第t个预测值和真实值,N代表总样本个数.
分析结果如表1所示:两个模型的RMSE相差近10倍,这进一步证明了本文提出的Logistic_SEIR模型的优越性.
由此可见:在预测现有确诊人数时,相比于SEIR模型,本文提出的Logistic_SEIR模型可以大量减少调参的数量,至多需要调试3个参数,而且不需要利
用额外的数据来分析和初始化参数,无论是从预测曲线还是RMSE的量化分析,本文的Logistic_SEIR模型都体现出了一定的优越性.
接下来本文进一步研究Logistic_SEIR模型需要调试的3个参数对模型预测效果的影响.
从预测曲线和加权误差两个角度分析不同初始健康人数S0对预测结果的影响.预测曲线如图3所示,加权误差如表2所示.
图3 不同初始健康人数S0的预测曲线
Fig.3 Prediction curves of different initial health population numbers S0
表2 不同S0初始值下误差计算
Tab.2 Error calculation of different initial values of S0
从图3可以直观地看出,时间越长各种初始值的曲线预测结果越相近,最后都重叠在一起.因此如果预测COVID-19发生2个月以后的现有确诊人数,则S0的初始值对预测效果影响不大,故Logistic_SEIR模型需要调试的S0参数可以比较容易地调试,这从另一方面证明了本文提出模型的优越性.
此外,从图3中可以看到,尽管各S0初始值模型最后的数据预测结果会重合,但整个过程中拟合的效果各不相同,比如对数据的峰值位置拟合最好的是曲线5,对峰值大小拟合最好的曲线1,峰值右侧下降部分则曲线7拟合得最好.为了定量分析曲线整体的拟合效果,本文提出了用加权误差,综合考虑曲线整体的拟合效果.加权误差的计算方法为:
加权误差=40%预测误差+30%峰值误差+
30%峰值位置误差,(7)
其中预测误差仍然用RMSE衡量,峰值误差、峰值位置误差都用绝对值误差衡量.绝对值误差的计算如公式(8):
Er=|y-p|,(8)
式中,y代表真实数据,p代表预测数据.
加权误差越小,模型的预测效果越好,由表2可知当S0=K×1.35时加权误差最小为1 816.42,预测效果最好.
从预测曲线和加权误差两个角度,研究由潜伏者转化为感染者的转化率α取不同初始值对曲线预测效果的影响.预测曲线如图4所示,加权误差如表3所示.
为了更准确地衡量哪个值最好,本文根据表3的加权误差来定量分析,可以看出潜伏者转阳变为感染者转化率α=1/4时加权误差最小,为1 816.42,预测效果最好.
从预测曲线和加权误差两个角度,分析不同初始康复率γ对预测结果的影响.预测曲线如图5所示,加权误差如表4所示.
从图5可以看到与不同S0初始值后半部分数据预测趋向重叠不同,对于不同的γ,后半部分数据预测曲线是不同的.本文通过对预测误差、峰值误差、峰值位置误差分别赋于40%,30%,30%的权重,得出加权误差来进行量化分析.根据表4的加权误差可知,γ=1/18时加权误差最小,为1 816.42,预测效果最好.
为了进一步说明不同康复率γ对本文提出模型性能的影响,在训练集和测试集不变的前提下又进一步在额外测试集上预测,预测结果如图6所示.
可以看到随着时间的增加,γ越大,预测效果越好.随着疫情的发展,治愈率越来越高,故随着时间的增加,γ值大的预测效果会更好.在实际预测过程中,可以在额外测试集上每隔4 d使γ值增加一些(比如从
图6 额外测试集上不同康复率γ的预测曲线
Fig.6 Prediction curve of different rehabilitation rates γ on additional test sets
1/18,1/16,1/14,…直到接近1).这从侧面证明了本文模型的优越性及良好的可解释性.
本文提出的Logistic_SEIR模型,克服了Logistic模型不能预测现有确诊人数的缺点,同时也解决了SEIR模型虽可以预测现有确诊人数,但需根据大量数据且需要多次调参的问题,把需要调参的数量从7个减少到3个.在实验部分,通过预测曲线和RMSE再次证明了本文提出的Logistic_SEIR模型比单独的SEIR模型优越.进一步研究Logistic_SEIR模型需要调试的3个参数对预测结果的影响,并指出该模型没有在其他数据集上测试,Logistic_SEIR模型参数的设置还不是完全的自动化,仍要手工微调一下,尤其是预测更长时间的现有确诊人数,需要对康复率进行调整(调高,比如每隔4 d,康复率从1/18,1/16,1/14,…逐渐调高,直到接近1),才能达到很好的预测效果.实现参数的完全自动设置是下一阶段的研究目标.