《厦门大学学报（自然科学版）》

在超临界CO2布雷顿循环系统设计中,为提高系统能量转换效率,需要准确预测风摩损耗.风摩损耗与转子转速、转子几何结构、工质状态密切相关.该文针对2 MPa CO2工质中,高转速(23 kr/min)转子的风摩损耗特性进行数值计算分析.研究结果表明:转子-定子壁面粗糙度对超临界CO2布雷顿循环系统中高转速以及可能出现的较高压强工况下的风摩损耗具有显著影响.已有风摩损耗经验关系式未考虑壁面粗糙度的影响,直接使用可能带来较大误差.风摩损耗随壁面粗糙度和转子转速的增加而增加,气腔宽度的变化对风摩损耗不会造成明显影响.

In order to improve the energy conversion efficiency of the supercritical CO2 Brayton cycle system,it is necessary to accurately predict the windage loss during the system design.Windage loss is closely related to rotor rotation speed,rotor geometry and the state of the working fluid.In this paper,the numerical calculation analysis of high-speed(23 kr/min)rotor windage loss characteristics in 2 MPa CO2 working fluid is carried out.The results show that rotor-stator wall roughness has a significant effect on the windage loss of the supercritical CO2 Brayton cycle under high rotation speed and high pressure conditions.The existing empirical relation of windage loss does not consider the influence of wall roughness,the direct use of which may cause considerable errors.The windage loss increases with both the wall roughness and rotor rotation speed.The cavity width between the rotor and stator does not have obvious influence on the windage loss.

引言
1 数值模拟计算模型
2 模型验证
3 结果分析
4 结论

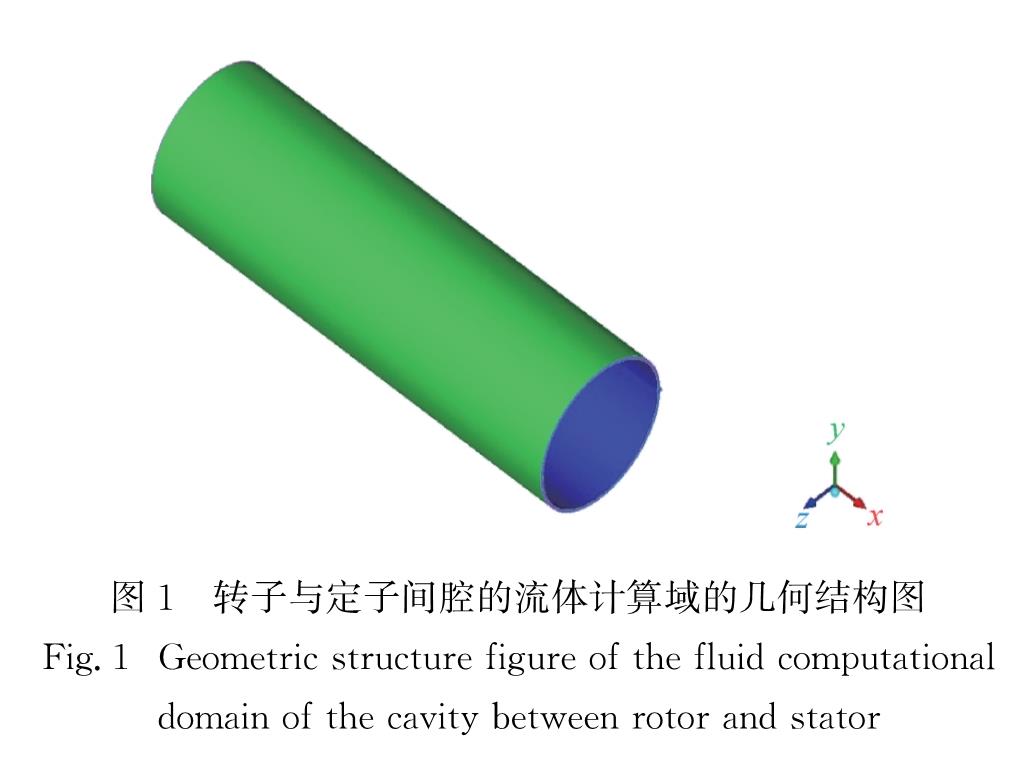
图1 转子与定子间腔的流体计算域的几何结构图<br/>Fig.1 Geometric structure figure of the fluid computational domain of the cavity between rotor and stator

图1 转子与定子间腔的流体计算域的几何结构图
Fig.1 Geometric structure figure of the fluid computational domain of the cavity between rotor and stator

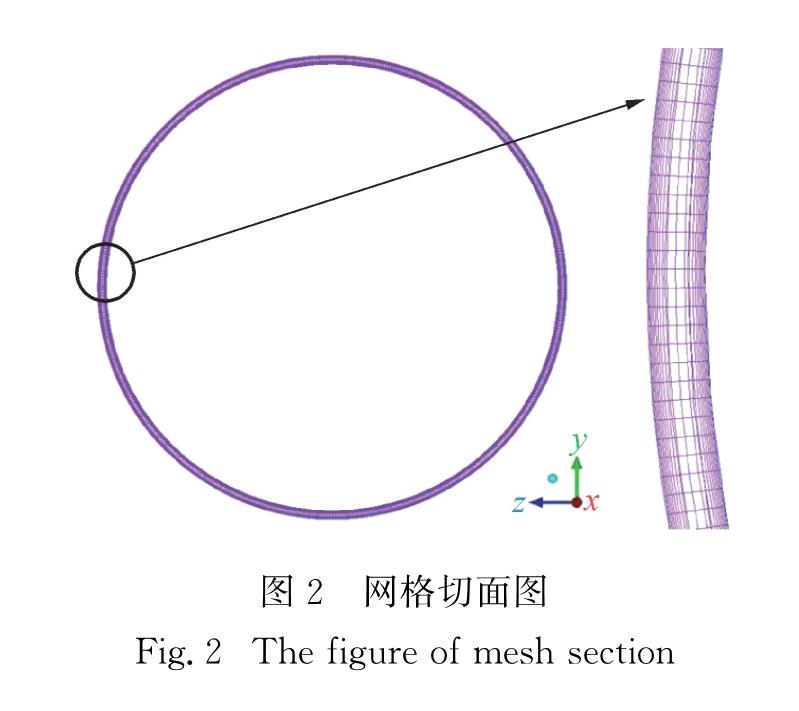
图2 网格切面图<br/>Fig.2 The figure of mesh section

图2 网格切面图
Fig.2 The figure of mesh section

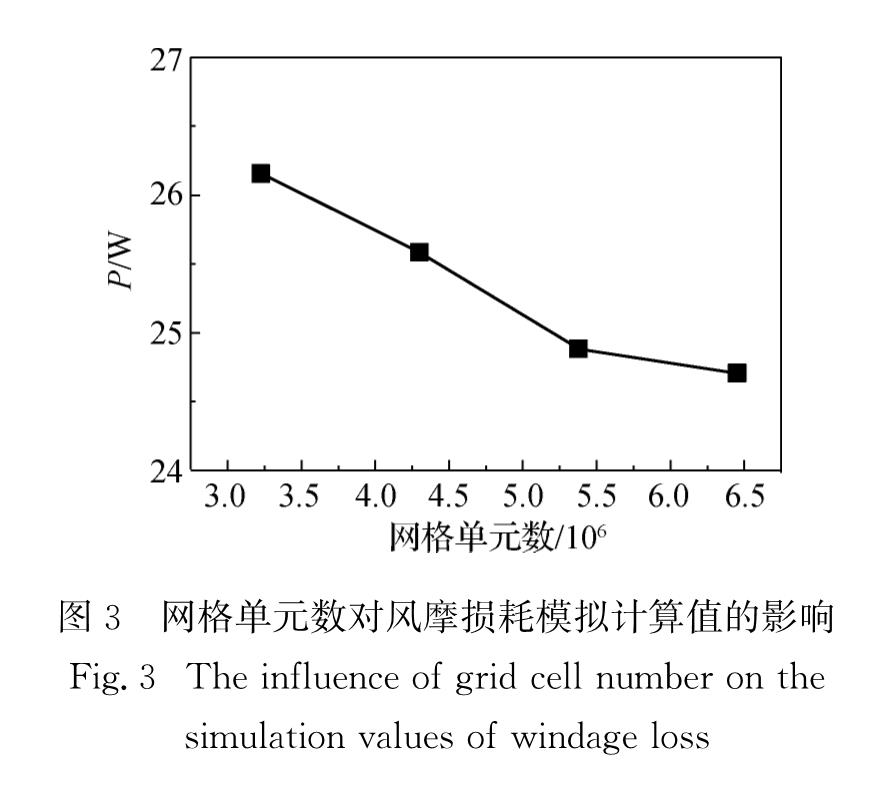
图3 网格单元数对风摩损耗模拟计算值的影响<br/>Fig.3 The influence of grid cell number on the simulation values of windage loss

图3 网格单元数对风摩损耗模拟计算值的影响
Fig.3 The influence of grid cell number on the simulation values of windage loss

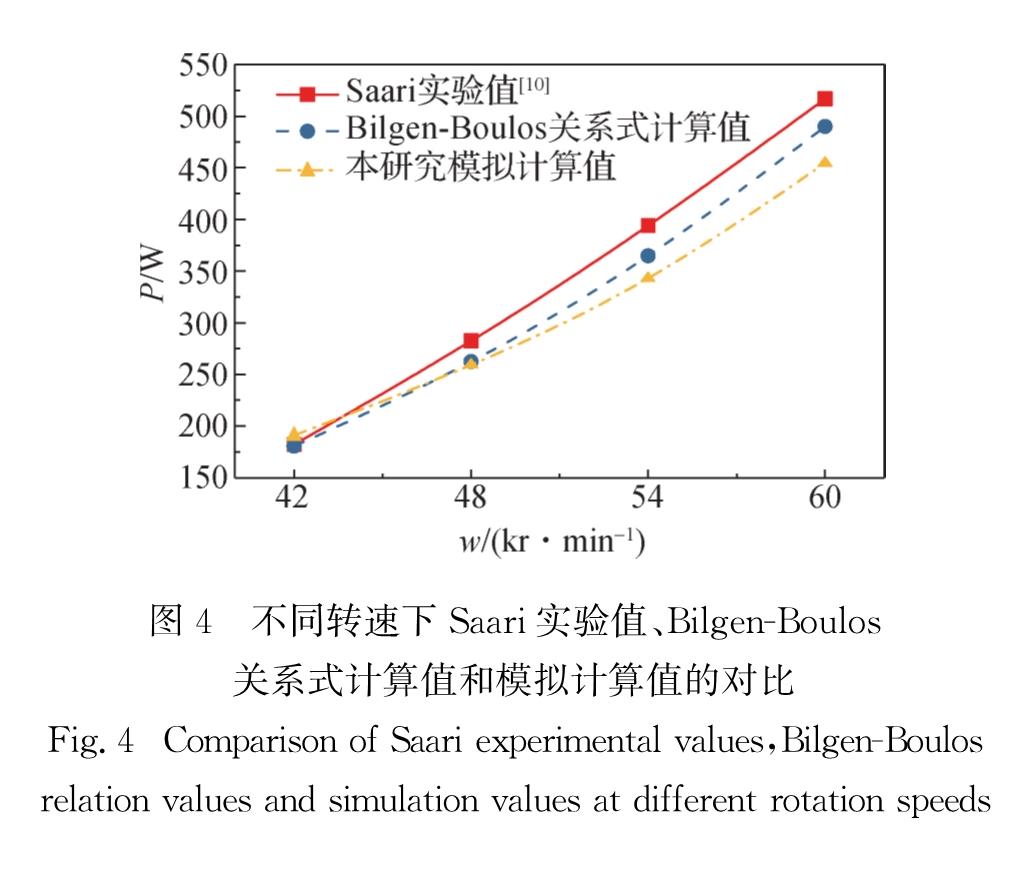
图4 不同转速下Saari实验值、Bilgen-Boulos关系式计算值和模拟计算值的对比<br/>Fig.4 Comparison of Saari experimental values,Bilgen-Boulos relation values and simulation values at different rotation speeds

图4 不同转速下Saari实验值、Bilgen-Boulos关系式计算值和模拟计算值的对比
Fig.4 Comparison of Saari experimental values,Bilgen-Boulos relation values and simulation values at different rotation speeds

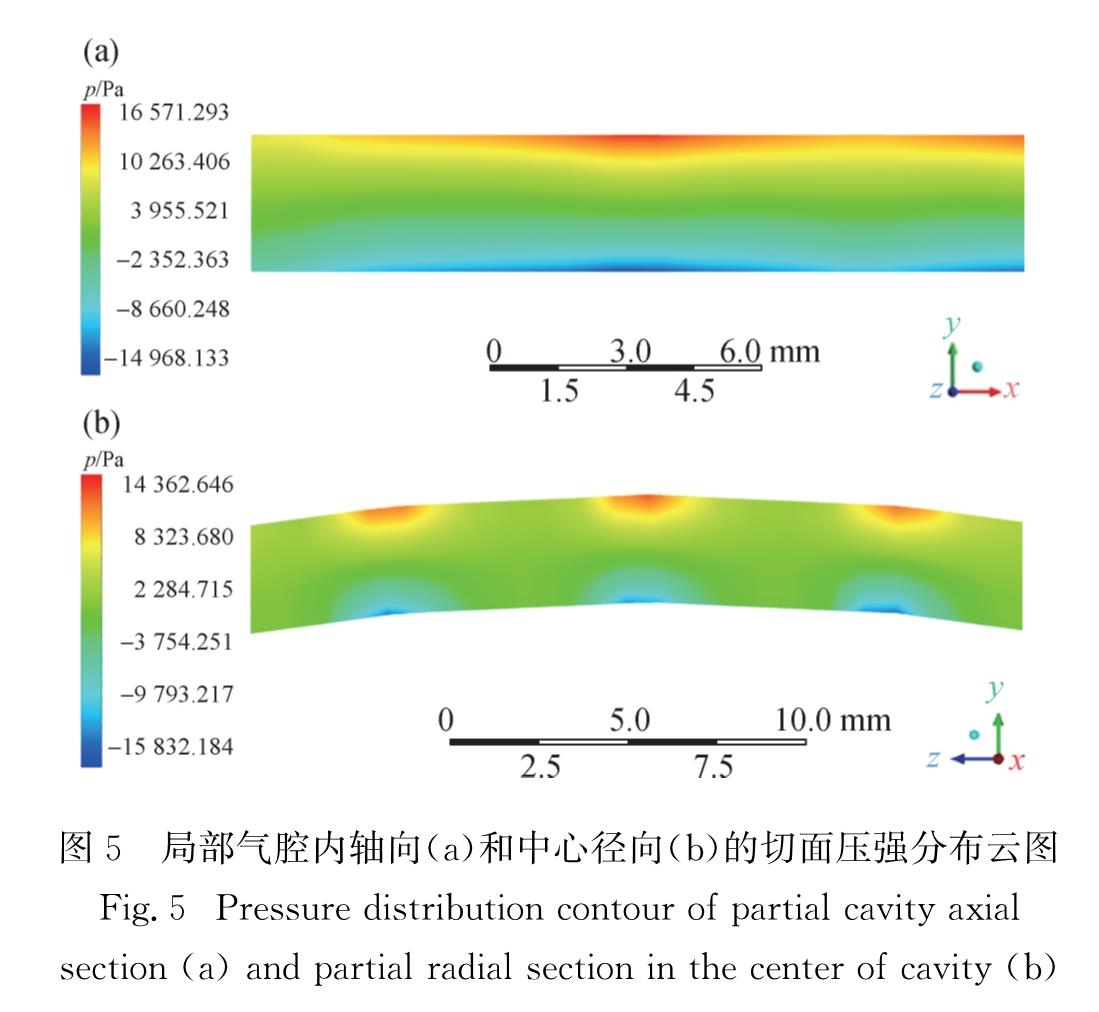
图5 局部气腔内轴向(a)和中心径向(b)的切面压强分布云图<br/>Fig.5 Pressure distribution contour of partial cavity axial section(a)and partial radial section in the center of cavity(b)

图5 局部气腔内轴向(a)和中心径向(b)的切面压强分布云图
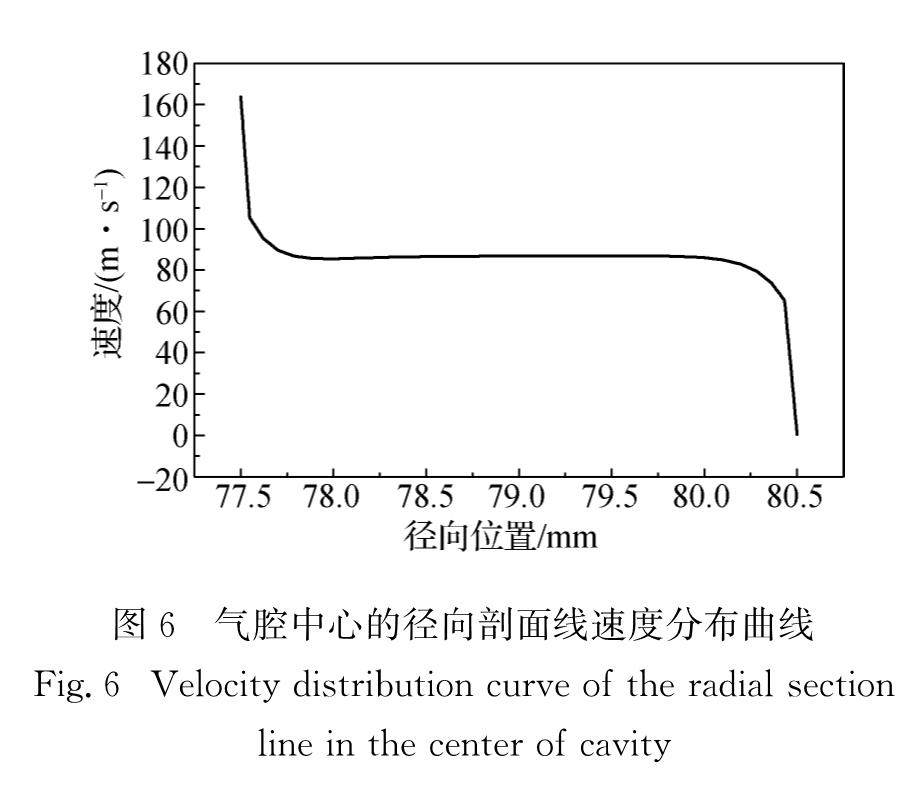
Fig.5 Pressure distribution contour of partial cavity axial section(a)and partial radial section in the center of cavity(b)

图6 气腔中心的径向剖面线速度分布曲线<br/>Fig.6 Velocity distribution curve of the radial section line in the center of cavity

图6 气腔中心的径向剖面线速度分布曲线
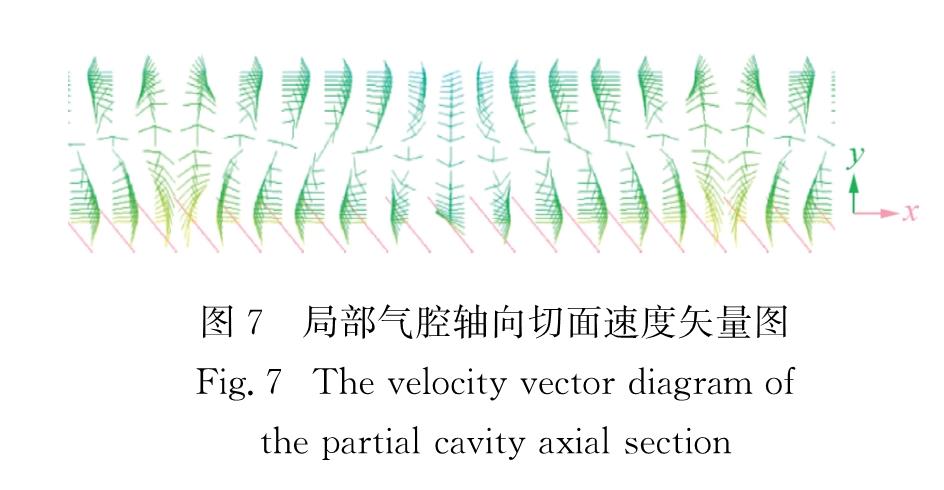
Fig.6 Velocity distribution curve of the radial section line in the center of cavity

图7 局部气腔轴向切面速度矢量图<br/>Fig.7 The velocity vector diagram of the partial cavity axial section

图7 局部气腔轴向切面速度矢量图
Fig.7 The velocity vector diagram of the partial cavity axial section

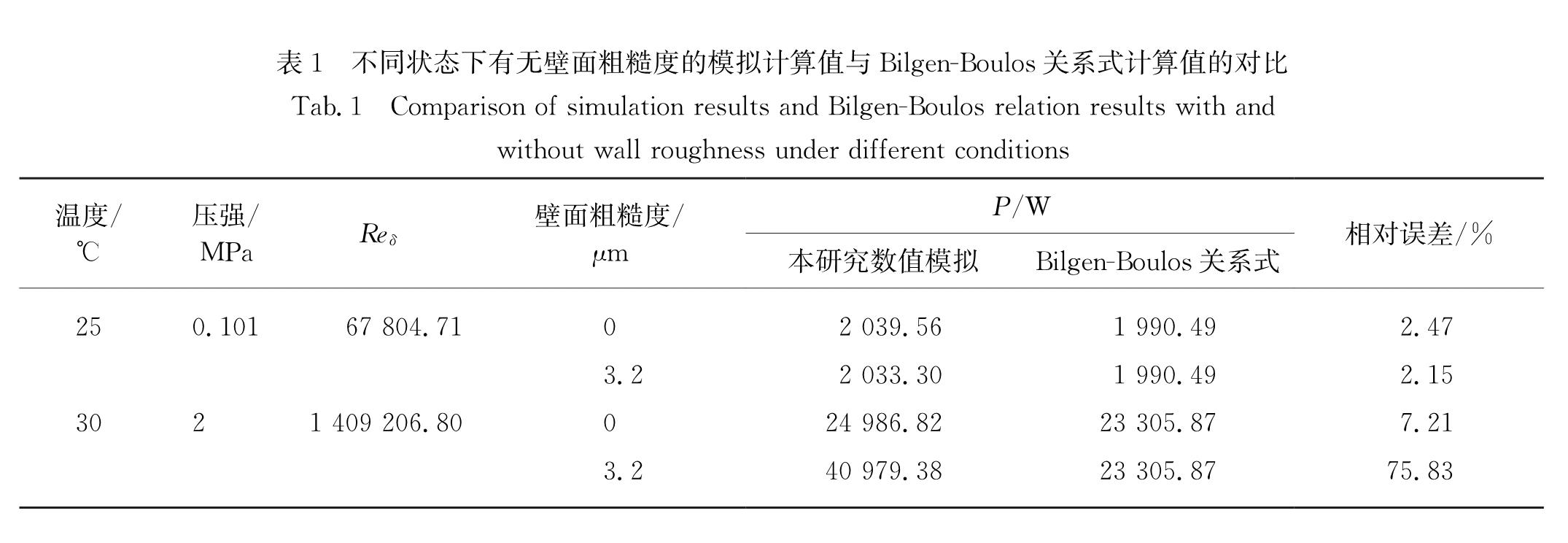
表1 不同状态下有无壁面粗糙度的模拟计算值与Bilgen-Boulos关系式计算值的对比<br/>Tab.1 Comparison of simulation results and Bilgen-Boulos relation results with and without wall roughness under different conditions

表1 不同状态下有无壁面粗糙度的模拟计算值与Bilgen-Boulos关系式计算值的对比
Tab.1 Comparison of simulation results and Bilgen-Boulos relation results with and without wall roughness under different conditions

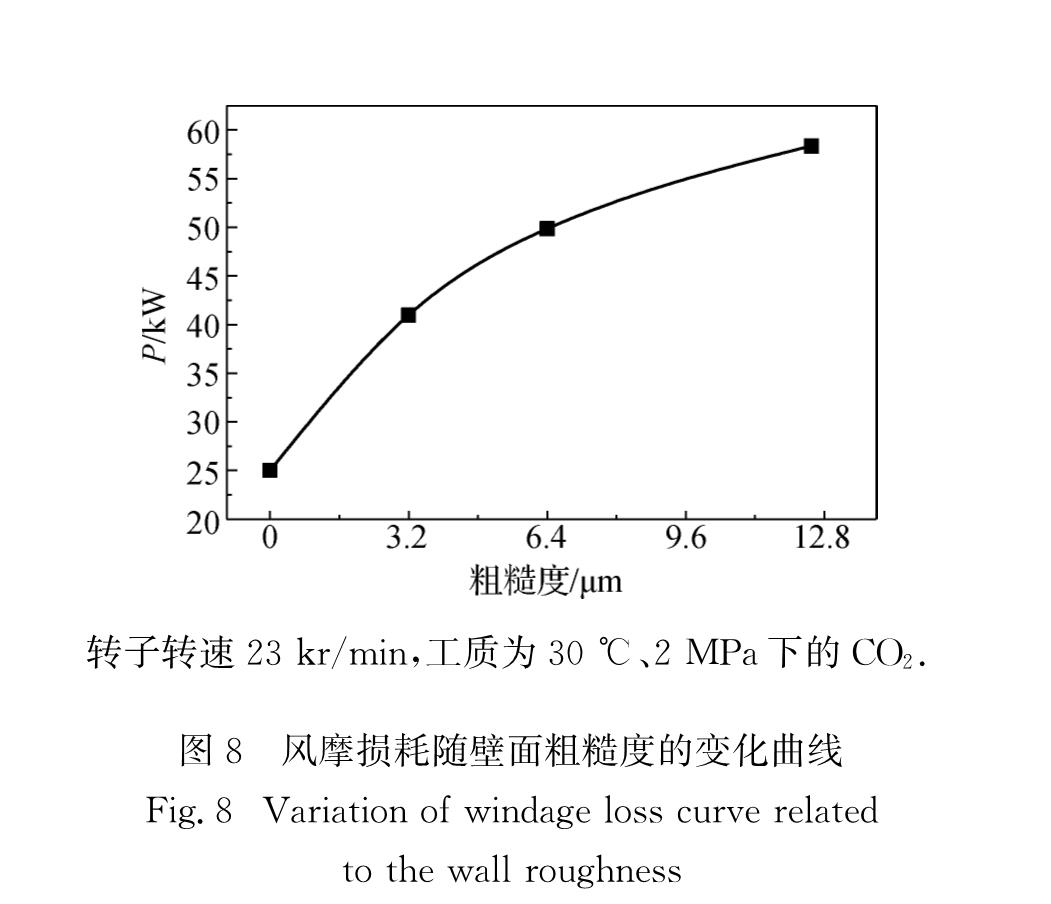
图8 风摩损耗随壁面粗糙度的变化曲线<br/>Fig.8 Variation of windage loss curve related to the wall roughness

图8 风摩损耗随壁面粗糙度的变化曲线
Fig.8 Variation of windage loss curve related to the wall roughness

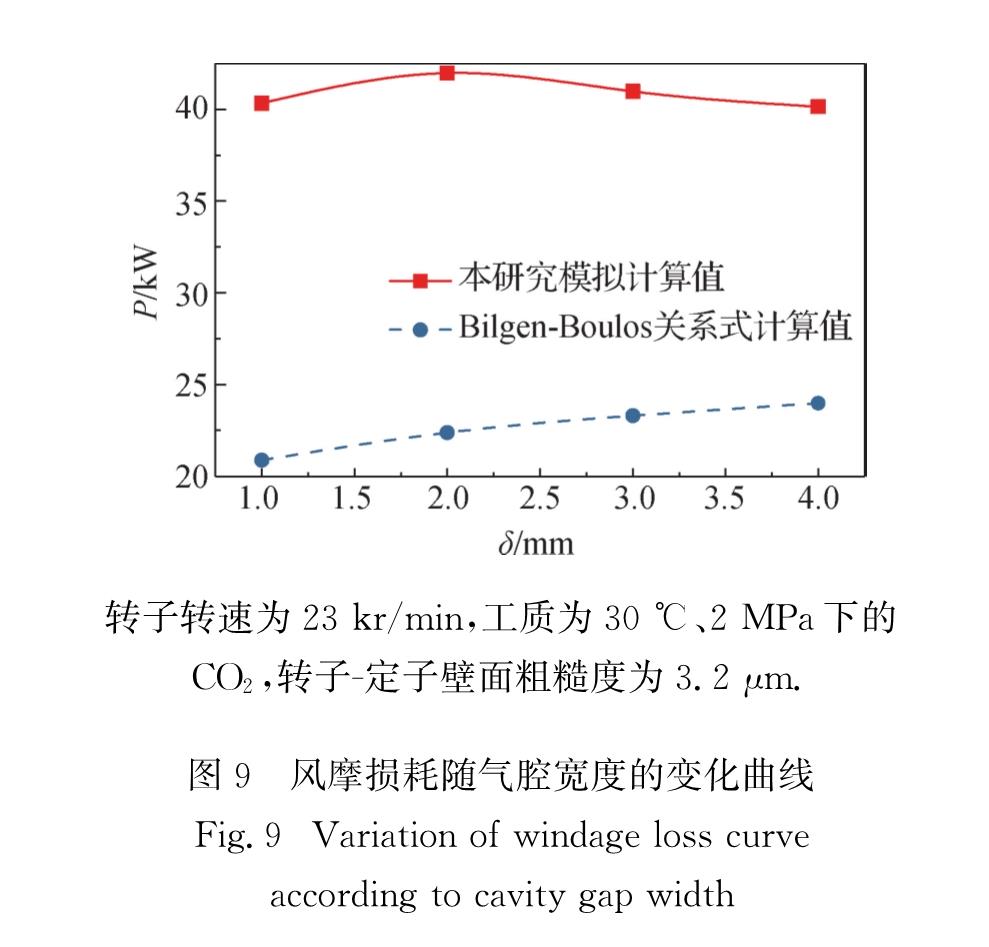
图9 风摩损耗随气腔宽度的变化曲线<br/>Fig.9 Variation of windage loss curve according to cavity gap width

图9 风摩损耗随气腔宽度的变化曲线
Fig.9 Variation of windage loss curve according to cavity gap width

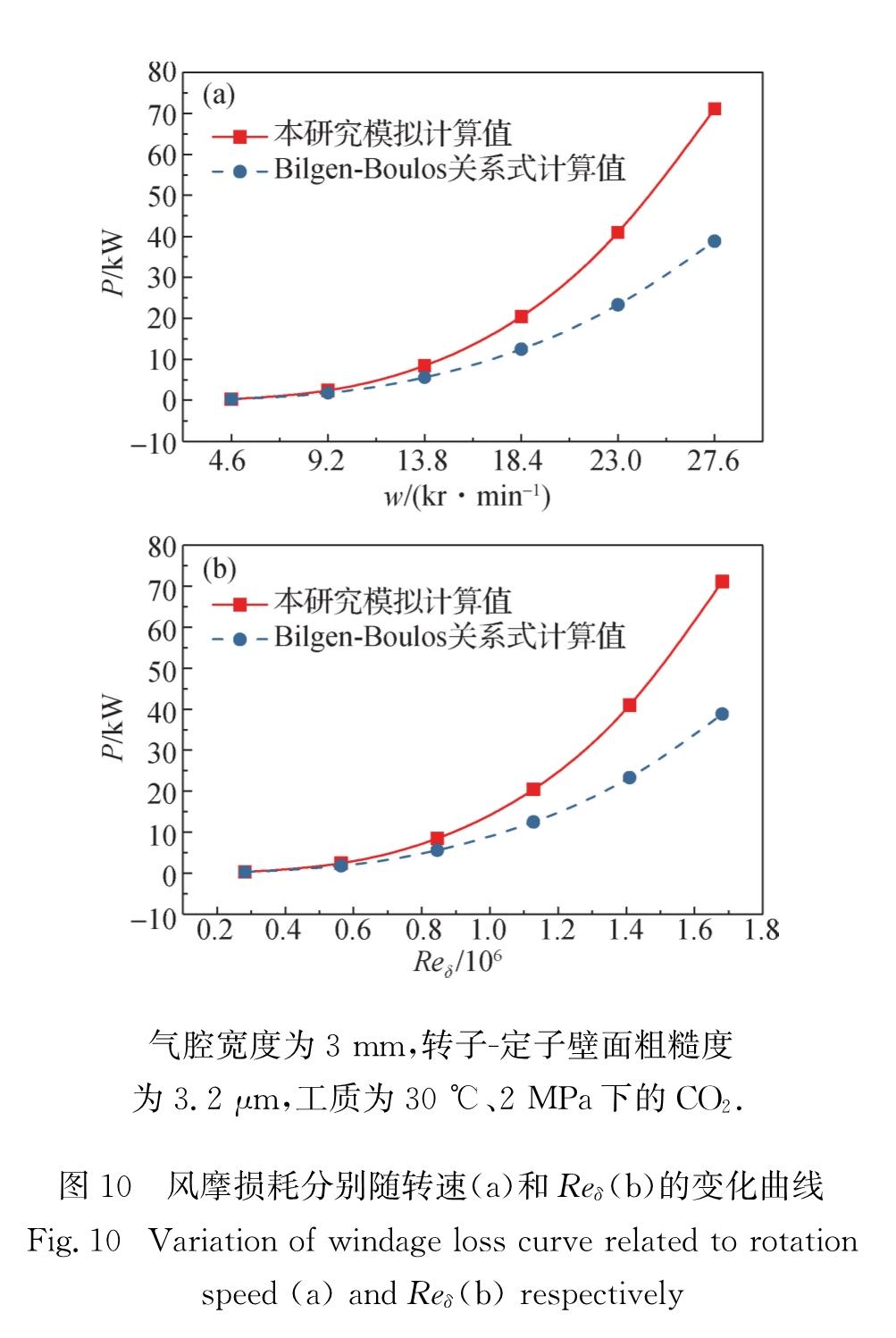
图10 风摩损耗分别随转速(a)和Reδ(b)的变化曲线<br/>Fig.10 Variation of windage loss curve related to rotation speed(a)and Reδ(b)respectively

图10 风摩损耗分别随转速(a)和Reδ(b)的变化曲线
Fig.10 Variation of windage loss curve related to rotation speed(a)and Reδ(b)respectively

[1] WENDT F.Turbulente Strömungen zwischen zwei rotierenden konaxialen zylindern[J].Ingenieur-Archiv,1933,4(6):577-595.
[2] TAYLOR G I.Fluid friction between rotating cylinders.Ⅰ.Torque measurements[J].Proceedings of the Royal Society of London Series A:Mathematical and Physical Sciences,1936,157(892):546-564.
[3] PANTELL K.Versuche über scheibenreibung[J].Forschung auf dem Gebiete des Ingenieurwesens,1949,16(4):97-108.
[4] DONNELLY R J.Experiments on the stability of viscous flow between rotating cylinders.Ⅲ.Enhancement of stability by modulation[J].Proceedings of the Royal Society of London Series A:Mathematical and Physical Sciences,1964,281(1384):130-139.
[5] DONNELLY R J,SIMON N J.An empirical torque relation for supercritical flow between rotating cylinders[J].Journal of Fluid Mechanics,1960,7(3):401-418
[6] YAMADA Y.Torque resistance of a flow between rotating co-axial cylinders having axial flow[J].Bulletin of JSME,1962,5(20):634-642.
[7] YAMADA Y.Resistance of a flow through an annulus with an inner rotating cylinder[J].Bulletin of JSME,1962,5(18):302-310.
[8] VRANCIK J E.Prediction of windage power loss in alternators[R].Ohio:Lewis Research Center,1968.
[9] BILGEN E,BOULOS R.Functional dependence of torque coefficient of coaxial cylinders on gap width and Reynolds numbers[J].Journal of Fluids Engineering,1973,95(1):122-126.
[10] SAARI J.Thermal analysis of high-speed induction machines[D].Helsinki:Helsinki University of Technology,1998:19-26.
[11] WRIGHT S A,RADEL R F,VERNON M E,et al.Operation and analysis of a supercritical CO2 Brayton cycle[R].Albuquerque:Sandia National Laboratories,2010.doi:10.2172/984129.
[12] 邢军强,王凤翔,张殿海,等.高速永磁电机转子空气摩擦损耗研究[J].中国电机工程学报,2010,30(27):14-19.
[13] 汪东欣.大型主氦变频驱动电机电磁设计方法研究与强度校核[D].哈尔滨:哈尔滨理工大学,2012:13-16.
[14] 丁树业,郭长光,郭保成,等.双馈水轮发电机风摩损耗数值研究[J].华中科技大学学报(自然科学版),2014,42(2):26-30.
[15] 张凤阁,杜光辉,王天煜,等.兆瓦级高速永磁电机通风系统设计与转子表面风摩耗研究[J].电机与控制学报,2014,18(2):50-55.
[16] 刘光伟,赵新刚,张凤阁,等.高速永磁爪极电机铁耗与空气摩擦损耗计算[J].电工技术学报,2015,30(2):148-154.
[17] 李玉超.280 kW高速感应电动机的设计与分析[D].沈阳:沈阳工业大学,2015:25-28.
[18] 李忠雨.感应电动机温升敏感性因素分析与优化[D].哈尔滨:哈尔滨理工大学,2016:25-29.
[19] 程文杰,李维,钟斌,等.高速电机定转子小间隙强迫风冷却数值模拟[J].微特电机,2018,46(11):6-11.

备注

引言

1 数值模拟计算模型

2 模型验证

3 结果分析

4 结论

学报简介

备注

引言

1 数值模拟计算模型

2 模型验证

3 结果分析

4 结 论

学报简介

4 结论