(Software School of Xiamen University,Xiamen 361005,China)Abstract:Quantitative market timing constitutes an important part of quantitative investment to choose the best trading opportunity.To verify the feasibility of applying hidden markov model(HMM)to
DOI: 10.6043/j.issn.0438-0479.201712002
备注
量化择时是量化投资领域的重要组成,主要负责评判何时进行交易.为了验证隐马尔科夫模型(hidden Markov model,HMM)应用到量化择时的可行性,基于股票市场原始数据计算得到候选特征集,并利用HMM对各个单特征进行特征筛选,最后使用选出的特征集训练得到综合模型,预测交易日的市场状态.实验结果表明,基于HMM的交易策略比双均线策略和基于k-均值(k-means)聚类的策略都有更好的表现,且具有较强的识别市场状态、规避系统性风险以及获取超额收益的能力.
Quantitative market timing constitutes an important part of quantitative investment to choose the best trading opportunity.To verify the feasibility of applying hidden markov model(HMM)to quantitative market timing,we creatively calculate candidate features set based on raw data,use HMM to test performance on each single feature,and train a comprehensive model using selected features to predict the market state of the next trading day.Experimental results show that HMM-based strategy enjoys better stability and profitability compared with strategies based on moving average or k-均值聚类算法的量化择时模型作为对比,对实验结果进行了分析,验证了HMM具有识别市场中长期状态的能力.HMM的主要原理在于马尔科夫性质的假设,相邻时序样本之间的关联信息能够被有效利用,隐状态的转换存在一定的概率分布,因而它能够选择合适的交易时机,并在市场迎来暴跌时有效保护资产组合.另外相较于其他两种常见策略,它在敏感性和稳定性上有更好的表现.
引言
精准预测金融市场是一件非常困难的任务,但是预测市场在未来一段时间的趋势或状态依旧是可行的.国内外许多文献已经指出,在金融市场尤其是股票市场和债券市场中,存在崩溃、缓慢成长、熊市和恢复阶段[1].De Angelis等[2]提出了检测市场稳定和混乱状态的框架模型,并且预测了两种状态之间的转换.Salhi等[3]使用隐马尔科夫模型(hidden Markov model,HMM)完成了金融危机和稳定时期的分类任务.与此同时,多种机器学习算法被应用于股票市场预测,如支持向量机(support vector machine,SVM)[4-6],神经网络[7],集成学习[8],深度学习 [9]等.Galeshchuk[7]发现了拥有最佳预测能力的神经网络,并用于交易所数据预测.Bebarta等[8]应用集成学习方法,组合人工神经网络、HMM和遗传算法构建了一个股票预测系统.并且随着深度学习的兴起与成熟,越来越多的研究开始利用深度神经网络进行股票涨跌预测 [9].然而由于为股票价格序列做标注难度较大,难以进行有效的监督学习,故HMM等非监督方法也被大量研究.Hassan等[10]利用HMM找到与预测当天最相似的历史数据,用以预测下一天的股价,为股票预测提供了一种新范式.之后,Park等[11]使用连续HMM预测下一天收盘价的变化方向.Seethalakshmi等[12]利用HMM识别股价的危机期和稳定期.但这些研究多数直接使用携带噪音更多的日内开盘价、最高价、最低价和收盘价作为模型的输入特征进行训练,没有在特征的选择上进行探究,并且没有充分发挥HMM对隐状态的刻画能力,也缺乏策略层面的充分验证.
为了在环境多变、难以预测的股票市场中研发可靠的量化交易策略,取代主观性较强的人工交易方式,有效地保障资产组合保值增值,本研究利用HMM自身特点来识别和预测市场状态,将可观察的特征作为观测值,将金融市场状态作为预测目标的隐状态.在此基础上,生成指数基金的量化交易策略,对策略的有效性通过各个层面予以评估,且通过与当前业内较为常用的基于技术指标以及基于无监督聚类的择时方法对比说明了该方法的有效性,同时也分析了这种方法的局限性和缺陷.
1 股票市场的HMM算法
图1 HMM量化金融示例
Fig.1 Example of HMM on quantitative finance股票市场周期可以粗略区分为牛市、熊市和震荡市,还能分成更多细粒度的市场状态,这些市场状态难以观察,且转换过程往往并非一蹴而就,存在一定的过渡期.图1为HMM模型量化金融示例图,HMM假设当前交易日t的市场状态st仅依赖于前一交易日状态st-1,故市场状态之间的转移概率分布为
P(st|st-1,st-2,…,s1,o1,o2,…,ot-1)=
P(st|st-1),(1)
其中ot为观测状态,这里可观测变量很多,一般表现为股价和成交量的波动,也可表现为一些技术指标的数值变化.进而,转移概率矩阵A可表示为
A=(aij)=(P(st=j|st-1=i)).(2)
市场状态st映射到观测状态ot的输出概率分布为
P(ot|st,st-1,…,s1,o1,o2,…,ot-1)=P(ot|st),(3)
B=(bjk)=(P(ot=k|st=j)).(4)
其中B为输出概率矩阵.根据HMM,在上述转移概率和输出概率的基础上,还需要有作为市场状态序列开端的初始状态概率分布π.
π=(πi)=(P(s1=i)).(5)
因此,股票市场可由一个完整的HMM模型θ=(A,B,π)的三元组描述.HMM的训练过程目前尚无最优解方法,一般采用鲍姆-韦尔奇(Baum-Welch)算法,根据期望-最大化(EM)原理确定局部最优的θ三元组.
预测过程则使用维特比(Viterbi)算法,定义状态空间为S={s1,s2,…st},令Vt,sk为在已有t个观测值下以状态sk为结尾的最可能状态序列的概率如式(6)和(7)所示,则当前状态st可由式(8)得到.
V1,sk=P(o1|k)·πk,(6)
Vt,sk=maxs∈S(P(ot|sk)·as,sk·Vt-1,st-1),(7)
st=argmaxs∈S(Vt,s).(8)
HMM保留了与当前交易日关联最强的前一交易日的信息,简化了建模过程,降低了模型复杂度; 且HMM相较于神经网络等其他模型来说具有更好的可解释性; 另外HMM也假设每个观测值仅依赖于当前的隐状态,该假设符合人们对于市场的理解认知.在牛市和熊市期间,市场的收益率和波动率分布具有显著差异 [13],因此有理由相信在不同市场状态下观测值拥有不同的分布.
总的来说,HMM拥有结构简单、鲁棒性强和可解释性好的优势,它在手写体识别[14-15]、体态识别[16]、自然语言处理[17-18]和语音识别[19]等时序相关领域的应用已经相当成熟; 其不足主要在于部分远期历史信息的丢失以及缺乏对每个状态的直接解释.
2 基于HMM的量化择时模型
模型整体流程如图2所示.首先,通过开源数据接口获取股票市场指数的原始日频历史行情数据,并从中计算得到相关候选特征.其次,为了能够找到拥有卓越盈利能力的特征,使用HMM对单个候选特征建模以进行回测检验,并根据评估指标选取有效特征.随后,利用有效特征集合对给定状态数的HMM模型进行训练.最后在回测阶段,模型被用于预测后一交易日的市场状态,并发出相应的交易信号.通过上述步骤,得到模型的最佳参数,并用于实际的量化交易中.
图2 模型流程图
Fig.2 Flow diagram of the model2.1 特征准备文中使用经过计算的特征取代前文所述的原始特征.在股票市场中,候选特征主要分为技术面特征和基本面特征两类.技术面特征主要是一些常用的技术指标,如相对强弱指数(relative strength index,RSI)、平均真实波动率(average true range,ATR)等,在这些指标的计算中往往对股价信息做了不同程度的平滑处理,在一定程度上减少了噪声,且这些指标在市场上被广泛运用多年,具有很强的可靠性.基本面特征主要是一些能够反映国家宏观经济状态的指标.上述特征都从各自的特定角度揭示了当前金融经济市场的状态.为了使模型更具通用性,本文中的主要研究对象为技术面特征.
2.2 特征筛选特征筛选的主要任务是从所有候选特征中挑选高质量的特征.不同特征从不同角度反映了市场状态,本文中将这些特征组合在一起以期能够起到互补效果,提高模型表现.
根据图2,在生成各个候选特征后,为每个特征构建单独的HMM模型并执行单特征检验.训练集上的单特征时间序列作为HMM模型的输入,可得到一个经过单特征训练的HMM模型,随后观察该模型在回测验证集上的预测表现.由于训练过程还涉及到状态数目的确定,本文中为每个单特征分别检验了状态数n∈[2,13]的回测情况,并对各个状态数下得到的回测结果的评估指标计算平均值获得该特征的综合回测性能表现.通过观察每个单特征模型在数据集上的回测表现,能够比较这些特征,评估它们的效用.在量化金融领域,常用年化收益率、最大回撤、夏普比率、交易胜率和交易频率等作为评估指标.年化收益率是衡量盈利能力的直接指标,而最大回撤是衡量模型可能遇到的最坏情况的有效指标,夏普比率衡量了单位风险水平下可获得的收益,交易胜率代表了盈利交易的比例,交易频率则衡量了交易成本的数量.在由专家给出指标的相对重要性后,评估指标RSI、平滑异同移动平均线(MACD)、ATR、资金流指标(MFI)、顺势指标(CCI)、乖离率指标(BIAS)的权重可由层次分析法获得,层次分析结构如图3所示.
图3 层次分析图
Fig.3 Analytic hierarchy process diagram评估出指标权重wi后,可计算每个特征的综合得分,可以得到
Score=∑ni=1wiei,(9)
其中,n为评价指标数量,ei为评价指标值.据此筛选得到表现靠前的K个特征,组合成训练特征集用于最终模型的训练.
2.3 状态识别HMM模型的输出包含多个状态区间如图4所示,为了识别出盈利和非盈利状态,需要在训练集上为每种状态执行多头策略(即在预测为该状态的交易日买入持仓,在非该状态的交易日卖出),并且统计它们各自的累积收益率曲线.
图4 状态区间
Fig.4 Interval of states一种简单的方法是根据在训练区间上统计得到的状态累积收益情况将状态分为2类,累积收益为正,代表可盈利状态,累积收益为负,代表不可盈利状态.根据状态所属类型,相应的执行多头或空头策略.若在考察期间共有T个交易日,第t个交易日的累积收益为rt,本文中识别可盈利状态的判定条件为:
rT>15%∨(rT>5%∧(t≤T,
rt>-3%)).(10)
式(10)定义的判定条件实际上代表了两类可盈利状态:第一类是具有明显盈利能力的状态,其收益率显著为正; 第二类是微盈利、小波动的状态,多数出现在震荡上行的行情.从长期来看,这两类状态都能够带来一定的利润.
一些盈利状态在某个特定时期可能会变得失效,一些状态也可能会从非盈利变为可盈利,这一方面是由于状态的含义不精准,导致状态识别存在一定的误差,另一方面也是由于市场本身的不稳定性造成的.尤其是当所选择状态数量多、比例大的时候,更有可能引入“不准确”状态.为了解决这个问题,采用一种直观的方法来满足需求——动态状态池.对每个状态在每个交易日进行监控,并根据式(10)条件进行检验,一旦某个状态满足条件,则将其加入到候选状态池中,相应地在该状态执行多头策略.相反,如果状态不能满足条件,则移出池子.
在状态识别的基础上,综合模型还需要确定最佳的状态参数.该步骤与单特征筛选的过程较为类似,主要通过分析一定范围状态数的综合模型在数据集上的回测验证结果,综合国家经济运行背景,选取其中状态区分度大,且盈利状态所获累积收益加和最高的状态数作为模型最终的状态参数.
2.4 回 测训练后的模型能够预测后一天的市场状态,根据预测得到的市场状态在相对应的指数交易所交易基金(exchange traded funds,ETF)上进行交易.交易规则如式(11)所示,pt+1为下一个交易日仓位,st+1表示预测的下一个交易日的市场状态类型,盈利状态为1,其他状态为0.
pt+1={1,st+1=1,
0,st+1=0.(11)
卓越的投资表现主要由以下3个因素构成:
1)回报率衡量投资组合获取绝对收益和超额收益的能力,也是一个交易策略的基本要求.通常用年化收益率和超额收益率来衡量回报率,它分别衡量投资策略获取盈利的速度以及战胜市场的能力.
2)风险也是一个重要的指标.一个稳定的策略能够规避糟糕的市场环境带来的巨大损失,低风险的策略能够做到低回撤.
3)交易成本也是需要考虑的因素之一.在大多数情况下,过量的交易会带来大量的无效交易.在中国,证券公司会对每笔交易收取成交额的0.15%作为佣金手续费,从长期来看,这是一笔巨大的开支并且会侵蚀一部分的利润.因此,保持相对高的胜率和控制合适的交易频率是必要的.
日频数据的使用也意味着本文中的策略是日频策略,策略模型监控每天的市场状态并且在下一个交易日做出相应的交易决策.添加仓位控制、止盈止损措施可以在很大程度上进一步将风险控制在更低的水平.
3 实 验
3.1 数据介绍为了简化实验,本文中选择市场指数作为实验对象,国内市场选取沪深300(CSI 300)指数,在国际市场选取标准普尔500(S&P 500)指数作为建模标的,其中选取跟踪CSI 300指数的300ETF(510300.OF)来模拟真实的交易场景.原始数据主要包含了交易日期、开盘价、最高价、最低价、收盘价、成交量、成交额信息.本研究选择CSI 300作为跟踪标的主要原因为:CSI 300是我国股票市场最为重要的交易指数之一,其跟踪标的流动性好,不易受到操纵,且波动性适中; 同时希望通过指数择时,能够为指数增强型基金产品提供一些新思路,以期获得超过纯被动型指数基金的超额收益.
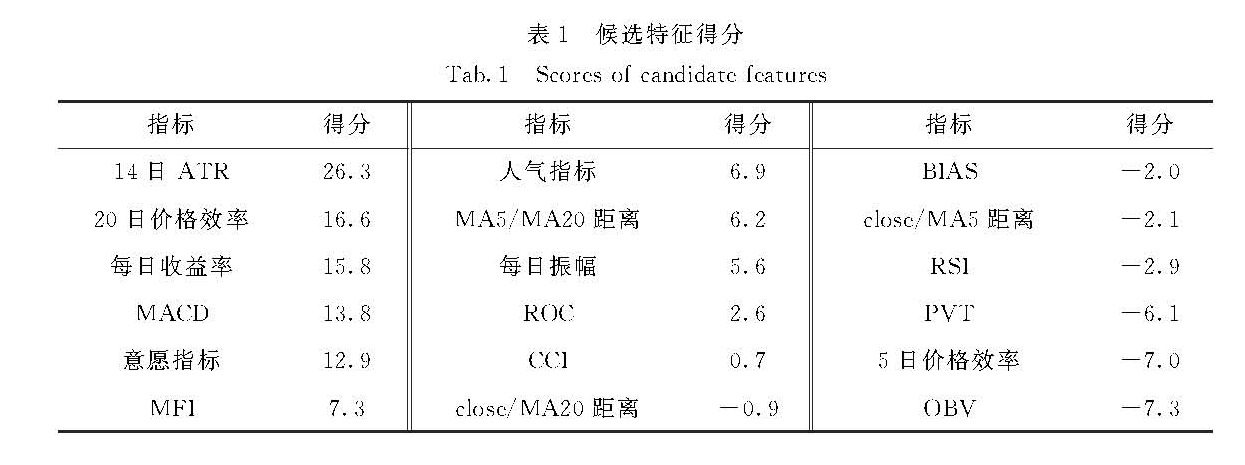
3.2 特征筛选如2.2节所述,本研究根据5个评价指标对18个候选特征进行综合打分并筛选特征.在保证一定盈利水平、可控制风险、维持一定的稳定性的目标下,由专家指导给出每个指标的重要程度分值,可得如式(12)所示的评估指标判断矩阵C.
C=[1 6/5 3/2 2 3
5/6 1 5/4 5/3 5/2
2/3 4/5 1 4/3 2
1/2 3/5 3/4 1 3/2
1/3 2/5 1/2 2/3 1].(12)
矩阵元素cij表示指标i相对于指标j的相对重要程度,矩阵自左向右和自上向下分别表示年化收益率、最大回撤、夏普比率、交易胜率、交易频率.通过对式(12)中的C进行特征向量分析,取最大特征值对应的特征向量进行归一化,即可得到每个指标具体对应的权重,本研究中上述指标最终权重向量W=(wi)=[0.30,0.25,0.20,0.15,0.10].其中最大回撤和交易频率指标是反向指标,因此在计算最终分值时需要给予负值处理.另外由于评价指标存在量纲不一致问题,需要在计算前进行标准化,主要依据各个评估指标的含义,以及其在量化投资领域常见的取值范围进行最大最小标准化(max-min normalization),夏普比率主要取值范围在(0,10),其余指标取值范围主要在(0,100),映射后可使所有指标不会带有额外的权重影响.
表1 候选特征得分
Tab.1 Scores of candidate features
表2 所选特征的平均测试结果
Tab.2 The average testing results of selected features3.3 状态识别如图5所示,将表2中选出的特征组合为每个交易日维度d=6的特征向量,作为综合HMM模型的输入.对于不同的市场,有不同的理想状态数.实验结果表明,一些状态可能从非盈利状态转换为盈利状态,意味着动态状态池是必要的.实际上,在模型中隐状态的含义是不确定的,隐状态可能代表了某段时期的赚钱效应,也可能代表了市场的波动率.在一定程度上,可以通过输入不同的特征集来控制隐状态的内在含义,这解释了为什么在表2中“每日收益率”的回测结果能够取得最高的累积收益率.
图5 组合特征
Fig.5 Combined features表3第1行为配合动态状态池并取得最佳回测表现的9状态HMM模型得到的结果,在回测过程中,动态状态池由3状态增加到4状态,说明其检测到了新的盈利状态.为了探索通过动态状态池能够获得的利润空间上限,引入未来函数对比实验结果.训练集被定义在2005—2013年,回测验证集定义为2014—2016年.通过直接观察2005—2016年间满足式(10)定义的条件的状态,得到一个包含未来信息的“未来状态集”.
图6 CSI 300指数走势图(2014—2016年)
Fig.6 Trend chart for CSI 300 index(2014—2016)
表3 9状态数HMM在CSI 300指数上的回测结果(2014—2016年)
Tab.3 Backtest results on CSI 300 index(2014—2016)of 9 states HMM表3中第2和3行分别展示了9状态模型在静态状态集中的预测能力和获取潜在更高累积收益的能力.对比静态状态集,对于大部分状态数模型,随着时间推移,在回测区间上至少出现一个能够获取收益的新状态,部分状态数模型甚至出现2～3个新增的候选状态,且这些新状态所带来的收益是非常显著的.从表3中可以看出,9状态动态状态池模型结果已经非常接近9状态下所能达到的最大潜在收益率105.14%,这说明动态状态池是有效且必要的.图6展示了CSI 300指数2014—2016年期间的市场运行情况,CSI 300指数基准收益率为43.95%,9状态模型获得了超过60%的超额收益.
为了检验本文中模型状态识别能力的通用性,也对模型在国际市场的表现进行了测试.由于本文中的股票特征具有明确的市场意义,其有效性具有一定的跨市场通用性,因此在国际市场中,直接使用3.2节中在国内市场上筛选得到的特征集.选取美国金融市场作为测试目标,实验中使用S&P 500指数2000—2006年期间的数据作为训练数据,2007—2016年作为回测集.表4给出了4状态HMM在S&P 500上的回测结果.状态数为3时,得到了236.63%的最大潜在累积收益,而指数的基准收益为140.27%.图7分别展示了HMM预测结果在回测区间上的状态转移情况和各个状态根据转移情况得到的净值曲线.从图7可知,长期而言,状态0,1代表了上升趋势,状态2代表市场反弹,同样可以带来利润.另外,
表4 S&P 500指数部分结果(2007—2016年)
Tab.4 Part of results on S&P 500 index(2007—2016)
图7 S&P 500指数4状态HMM模型
Fig.7 4-states HMM model for S&P 500 index状态1在开始阶段经历了损失,直到2009年才成为一个候选状态,而后为整个资产组合带来了利润.状态3代表了剧烈的下跌趋势.可以看到训练后的HMM模型避免了2008年金融危机给股市带来的剧烈下跌.受益于更加成熟的市场环境,在美国市场只需要更少的状态就能够充分描述市场变化,获取稳定收益.
3.4 结果分析文中将基于HMM的量化择时模型与基于双均线技术指标、基于k-均值聚类算法的量化择时模型进行了性能对比.
1)基于双均线技术指标的量化择时模型
移动平均线是股票和期货市场上历史最为悠久、应用最为广泛的技术指标之一,基于均线的择时策略也因其简单易懂而广泛运用.双均线策略主要利用短期移动平均线和长期移动平均线之间的相对位置关系发出交易信号 [20-21],短期均线运行在长期均线上方则视为持仓信号,反之则视为空仓信号.均线模型主要涉及的参数为长短期均线的周期.
2)基于k-均值聚类算法的量化择时模型
近年来,已有研究将机器学习方法运用在量化投资领域[22].本文中基于k-均值聚类算法将每天的特征向量作为对每个交易日的描述,并将欧式距离作为样本间相似度的度量标准,将拥有相似特征的相似交易日进行聚类并预测为同一种市场状态,根据预测得到的状态发出相应交易信号.
3种方法的比较结果如表5所示.通过组合长短期均线周期(5/10/20/30/60),对双均线择时模型共10个参数组合进行了测试,MA10/MA60参数组合获得了最佳表现.在2014—2016年期间,该模型共发生6笔交易,获得23.73%的年化收益率,此时最大回撤25.68%.从结果上看,双均线策略的平均最大回撤率分别比HMM高出16.5个百分点,比k-均值聚类算法高出13.56个百分点,均线策略本身的延迟性造成了幅度更大的回撤区间.利用表2中的特征对基于k-均值聚类算法的量化择时模型进行测试.在没有使用动态状态选择的情况下,5状态k-均值聚类算法在2014—2016年期间取得了15.19%的年化收益率和对应13.29%的最大回撤.通过使用动态状态选择,8状态k-均值聚类算法能够带来84%的潜在收益,对应最大回撤仅12.74%.不过在大多数情况下,其胜率都低于50%,且交易频率偏高.
表5 3种方法统计结果
Tab.5 Statistical results of 3 methods综合对比结果可知,HMM拥有参数少、鲁棒性强和可解释性强的优势.从最大回撤率的角度来看,基于HMM的策略的表现皆优于k-均值聚类算法和双均线策略,表明相较于其他常见策略,HMM在规避风险的敏感性和在控制回撤的有效性上表现更佳.从期望收益率的角度看,基于HMM的策略的表现优于k-均值聚类算法,与均线策略相当.这主要源于HMM合理的马尔科夫性质假设.另外,HMM策略带来了长期高于50%的交易胜率,以及更低的交易频率.从平均意义上来说,它产生更少的交易费用.
均线策略的最大缺陷来源于均线的延迟性,这会在趋势不明显的震荡市带来长期的亏损.只有在趋势明显的牛市或熊市期间均线策略才能够带来大幅利润或避免大幅损失.然而通常来说,在经济周期的影响下,市场每经过7～8年才会有一轮趋势明显的牛市或熊市,因此均线策略所需回报周期更长.另外,找到合适的均线参数也是相当困难的,很容易造成过拟合.而k-均值聚类算法则完全没有考虑相邻交易日之间的关系,导致了频繁的状态转换和高昂的交易成本.
4 结 论
本研究围绕量化投资领域的量化择时问题,研究了HMM在该领域的应用,给出了如何基于HMM构建量化交易策略的完整流程.同时将基于移动平均线和k-均值聚类算法的量化择时模型作为对比,对实验结果进行了分析,验证了HMM具有识别市场中长期状态的能力.HMM的主要原理在于马尔科夫性质的假设,相邻时序样本之间的关联信息能够被有效利用,隐状态的转换存在一定的概率分布,因而它能够选择合适的交易时机,并在市场迎来暴跌时有效保护资产组合.另外相较于其他两种常见策略,它在敏感性和稳定性上有更好的表现.
尽管HMM在量化择时上有较为优越的表现,但是仍然存在一些不足,在后续的研究中将进一步改进.
1)当前模型的状态选择依然属于静态规则,不能有效监控各个状态的动态变化.当某个状态当前不能满足特定条件时,很容易错过巨额的利润空间,而满足条件时,又很容易遭遇巨幅回撤,也即在动态状态监控上存在滞后.因此需要对动态状态选择机制进行进一步的智能优化.
2)择时往往只是一个量化交易系统的一部分,通过合理利用策略融合技术,将隐马尔科夫择时模型与其他的策略组合使用,充分利用择时模型对市场环境的预判能力,能够更加有效地挖掘个股股价的利润空间,规避市场风险.
3)本文中提出的策略流程,尚未考虑任何仓位控制和止盈止损措施,如何合理通过添加风险控制措施来提高策略的可控性也是重要的研究课题.
4)当前针对的主要跟踪交易对象为市场指数,在后续研究中,将进一步针对预测难度更大的个股以及期货品种进行模型研究.
- [1] GUIDOLIN M,TIMMERMANN A.Asset allocation under multivariate regime switching[J].Journal of Economic Dynamics & Control,2007,31(11):3503-3544.
- [2] DE ANGELIS L,PAAS L J.A dynamic analysis of stock markets using a hidden Markov model[J].Journal of Applied Statistics,2013,40(8):1682-1700.
- [3] SALHI K,DEACONU M,LEJAY A,et al.Regime switching model for financial data:empirical risk analysis[J].Physica a-Statistical Mechanics and Its Applications,2016,461:148-157.
- [4] 杨新斌,黄晓娟.基于支持向量机的股票价格预测研究[J].计算机仿真,2010,27(9):302-305.
- [5] 谢国强.基于支持向量回归机的股票价格预测[J].计算机仿真,2012,29(4):379-382.
- [6] CAO L,TAY F E H.Financial forecasting using support vector machines[J].Neural Computing & Applications,2010,10(2):184-192.
- [7] GALESHCHUK S.Neural networks performance in exchange rate prediction[J].Neurocomputing,2016,172(C):446-452.
- [8] BEBARTA D K,SUDHA T E,BISOYI R.An intelligent stock forecasting system using a unify model of CEFLANN,HMM and GA for stock time series phenomena[C]∥Emerging Ict for Bridging the Future.Berlin:Springer-Verlag Berlin,2015:485-496.
- [9] 李文鹏,高宇菲,钱佳佳,等.深度学习在量化投资中的应用[J].统计与管理,2017,9(8):104-106.
- [10] HASSAN R,NATH B.Stock market forecasting using hidden Markov model:a new approach[C]∥5th International Conference on Intelligent Systems Design and Applications.Los Alamitos:IEEE,2005:192-196.
- [11] PARK S H,LEE J H,SONG J W,et al.Forecasting change directions for financial time series using hidden Markov model[C]∥Rough Sets and Knowledge Technology.Berlin:Springer,2009:184-191.
- [12] SEETHALAKSHMI R,KRISHNAKUMARI B,SAAVITHRI V.Gaussian kernel based HMM for time series data analysis[C]∥Conference Proceedings of 2012 International Conference on Management Issues in Emerging Economies.Thanjavur:IEEE,2012:105-109.
- [13] 李腊生,翟淑萍,关敏芳.证券市场收益率分布时变性的经济学分析及其我国的经验证据[J].统计研究,2011,28(11):66-78.
- [14] FIERREZ J,ORTEGA-GARCIA J,RAMOS D,et al.HMM-based on-line signature verification:feature extraction and signature modeling[J].Pattern Recognition Letters,2007,28(16):2325-2334.
- [15] 肖明,贾振红.基于轮廓特征的HMM手写数字识别[J].计算机工程与应用,2010,46(33):172-174,211.
- [16] CHEN F S,FU C M,HUANG C L.Hand gesture recognition using a real-time tracking method and hidden Markov models[J].Image and Vision Computing,2003,21(8):745-758.
- [17] KHAN W,DAUD A,NASIR J A,et al.A survey on the state-of-the-art machine learning models in the context of NLP[J].Kuwait Journal of Science,2016,43(4):95-113.
- [18] 韩普,姜杰.HMM在自然语言处理领域中的应用研究[J].计算机技术与发展,2010(2):245-248,252.
- [19] PARAMONOV P,SUTULA N.Simplified scoring methods for HMM-based speech recognition[J].Soft Computing,2016,20(9):3455-3460.
- [20] 谭磊.趋势跟踪类策略的内在逻辑[J].当代经济,2017,27(6):144-145.
- [21] 景泰然.量化投资在期货交易中的应用[J].现代商业,2015,12(18):152-153.
- [22] 张文俊,张永进.4种数据挖掘典型分类方法在股票预测中的性能分析[J].安徽工业大学学报(自然科学版),2017,34(1):97-102.
