为解决BIT*方法中存在因路径代价下降速度慢导致规划时间长、效率不佳的问题,本文提出了WB-BIT*方法.
1.1 函数定义
路径规划是指在地图中寻找到一条安全且可行的连接起始点和目标点的路径.对于移动机器人,其路径代价可等同于移动的距离,因此在本文后续章节中使用路径长度代表路径代价.定义X∈Rn表示为移动机器人的状态空间,n为搜索空间的维度.BIT*方法在状态空间里呈树状增量搜索,采样点连接至搜索树后成为节点v,两节点间的连接称为搜索树的边.搜索树T包含了节点集合V和边集合E,即T=(V, E).定义搜索树T中起始点xstart到目标xgoal的最优路径长度为cbest,当前路径长度为ci,未找到可行路径时ci=∞.
定义函数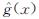 和
和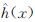 分别表示从起始点到点x、从点x到目标点的估计长度,其中x∈X.定义函数gT(x)表示从起始点到点x在搜索树T中的实际长度.估计长度通常为两点间的欧几里德距离.
分别表示从起始点到点x、从点x到目标点的估计长度,其中x∈X.定义函数gT(x)表示从起始点到点x在搜索树T中的实际长度.估计长度通常为两点间的欧几里德距离.
定义函数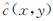 和c(x,y)分别表示点x到点y的估计长度和实际长度,其中x,y∈X.此外,当边(x,y)与障碍物相交时,视作发生碰撞,此时认为c(x,y)=∞.
和c(x,y)分别表示点x到点y的估计长度和实际长度,其中x,y∈X.此外,当边(x,y)与障碍物相交时,视作发生碰撞,此时认为c(x,y)=∞.
1.2 WB-BIT*方法主要模块
WB-BIT*方法的整体结构框架具体如算法1所示,其中包含了以下几个主要模块:
1)批量均匀和偏置采样.WB-BIT*方法首先在整个搜索空间中随机均匀采样; 当获得初始路径后,以目标点和起始点为焦点,初始路径长度作为长轴长度构建的椭圆区域称为知情集,如图1所示; 当知情集确定后,采样则在此椭圆区域中进行,该区域会随当前最优路径长度的减少而逐步缩小.本文设计了基于路径指导的偏置采样,与当前椭圆区域的均匀采样相结合,以此减少原始椭圆区域中可能存在的冗余样本,同时有效利用路径信息,提高探索路径的效率,即算法1中第7行.
图1 知情集采样区域
Fig.1 Informed set sampling region
2)边的预扩展与选择.队列QV是以当前搜索树中节点v∈V的连接长度与目标估计长度之和递增排序,即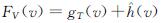 ; 队列QE则是边(v, x)通过当前搜索树中连接长度与(v,x,xgoal)三点间估计长度之和递增排序,即FE(v,x)=gT(v)+
; 队列QE则是边(v, x)通过当前搜索树中连接长度与(v,x,xgoal)三点间估计长度之和递增排序,即FE(v,x)=gT(v)+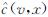 +
+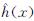 ; QV和QE各自队列中的最小值代表其所在队列的最优值.当节点v的最优值不大于队列QE的最优值时,该节点才在自身连接半径内进行边的预扩展,避免不必要的冗余计算花费.在节点预扩展完成后,QE队列选择并移除具有最小值的边(vmin,xmin),进行实际扩展的准备,如算法1第10~12行.WB-BIT*的连接半径与BIT*一致,即rWB-BIT*=rBIT*,其表达式为:
; QV和QE各自队列中的最小值代表其所在队列的最优值.当节点v的最优值不大于队列QE的最优值时,该节点才在自身连接半径内进行边的预扩展,避免不必要的冗余计算花费.在节点预扩展完成后,QE队列选择并移除具有最小值的边(vmin,xmin),进行实际扩展的准备,如算法1第10~12行.WB-BIT*的连接半径与BIT*一致,即rWB-BIT*=rBIT*,其表达式为:
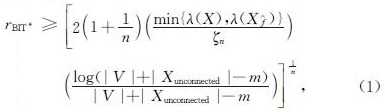
其中:m为每一批次采样点的数量,λ(·)是集合的勒贝格测度,Xf∧代表当前知情集搜索区域,ξn代表n维单位球的勒贝格测度,Xunconnected表示还未连接至搜索树的采样点集合.
3)节点与边的扩展和路径优化.选择的边(vmin,xmin)在通过启发式和碰撞检测的判断后,才会进行实际扩展,连接并加入搜索树中(算法1第13~23行).此时若点xmin已存在于搜索树中,则认为是树的重布线过程,否则该点加入节点集合V,并判断其是否能连接至目标点,若能连接,即可输出一条可行路径及其长度.本文设计了一种路径包围优化策略,每当路径长度发生变化时能够利用该策略将当前路径快速包围至障碍物周边,使路径长度快速减少,有效缩小知情集的椭圆区域,从而提高搜索精度(算法1第20行).
4)节点与边的修剪.每批次采样点处理完成后,当前已有节点计算实际长度gT(v)与目标估计长度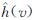 之和,计算结果大于当前最优路径长度ci的节点将被修剪删除; 采样点中
之和,计算结果大于当前最优路径长度ci的节点将被修剪删除; 采样点中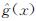 与
与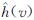 之和大于ci的点也会被修剪删除.当被修剪的节点位于知情集区域中,则认为其还存在提供更优连接至目标的可能性,将在下一批采样中被重新使用(算法1第6、8行).
之和大于ci的点也会被修剪删除.当被修剪的节点位于知情集区域中,则认为其还存在提供更优连接至目标的可能性,将在下一批采样中被重新使用(算法1第6、8行).
算法1 WB-BIT*

1.3 路径包围优化
在路径规划过程中,知情集是通过当前最优路径长度决定采样区域的大小,而更小的采样区域能够提供更精细的搜索.因此,为了通过减小采样区域实现更加精细的搜索和更短路径的获取,本文设计了一种基于当前路径包围障碍物的路径优化策略.该优化策略主要流程如算法2的伪代码所示.
算法2 Path_Optimization(Xpath,r)
算法2的路径优化策略在路径长度有更新时执行.策略开始执行后,当前路径根据自定义变量被离散为均匀配置,由目标点至起始点将路径包围至障碍物周围.算法2伪代码中的LocalPath()函数表示节点之间连线的碰撞检测,|Xpath|表示路径点集合的基数,若路径中包含N个点,则Xpath={x1,x2,…,xN}.此外,算法2中U是路径连接的离散化程度,根据当前连接半径与自定义变量的比例来确定,能在路径点连接大于连接半径时更精细地进行路径优化.
图2展示了一个简单的路径优化示例,图2(a)黑色实线为原始路径.首先拟连接xgoal和x1(蓝色虚线),当此连接发生碰撞时,通过均匀离散化拟连接直到x'2与x1和xgoal的连接均在可行区域(图2(b)),此时x'2替换x2作为新的连接,如图2(c)红色实线所示.然后重复类似过程得到x'1,最后得到图2(d)所示的新路径.显然,由于三角不等式中第三边小于其余两边之和,优化后的路径具有更短的长度.
图2 路径包围优化过程
Fig.2 Wrapping process of path optimization
1.4 基于路径指导的偏置采样
路径优化策略能够加速当前路径长度的减少,获得一条高质量路径.当环境中存在多条路径时,则需要保持对潜在更优新路径的探索.因此,本文设计了一种采样策略,利用当前路径点相关的启发式函数值计算搜索区域,执行偏置采样.
WB-BIT*方法探索初期未找到路径时,路径长度视为无穷大,采样在整个搜索空间中随机均匀进行.当获得一条可行路径时,偏置采样策略才会执行.可行路径是由各路径点连接而成,可表示为Xpath={xstart,x1,x2,…,xgoal},策略首先计算各路径点的启发式值:
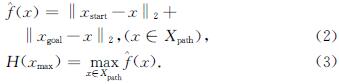
其次取各点启发式值中最大值H(xmax)作为偏置采样的参数,使用H(xmax)作为椭圆长轴的长度,起始点xstart和目标点xgoal作为焦点建立一个椭圆的偏置采样区域,如图3所示.所建立的偏置采样区域属于知情集的子集,在路径数量不止一条的情况下,从这个较小子集中进行采样,更有可能找到改善路径和加快算法收敛的采样点.然而,由于该采样区域是通过现有路径进行估计的,所含信息不如知情集充足,可能得到的是局部最优路径[19].因此,为了确保WB-BIT*方法的采样均匀性而保证渐进最优性,偏置采样需要与知情集采样结合,并引入偏置比α∈(0,1)来平衡这一采样过程(如算法3第7行).当已有可行路径时,在偏置区域生成样本的概率为α,在知情集中进行采样的概率则为1-α.偏置采样的伪代码如算法3所示.
算法3 Hybrid_Sample(m,xstart,xgoal,ci,Xpath)

图3 知情集采样与偏置采样
Fig.3 Informed sampling and biased sampling
1.5 理论分析
本小节对WB-BIT*方法进行理论分析.
定理1 概率完备性.对于待解决路径规划问题,若该问题存在解,则当方法的迭代次数或搜索时间趋于无穷大时,获得一条从起点到终点的可行路径解的概率为1,即:
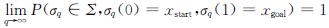 ,
,
其中:q是采样点的数量,σq是从这些采样点中找到的路径,Σ是所有可行路径的集合.
证明 WB-BIT*是基于BIT*方法的改进,通过节点扩展和连接增量地生成连续的树.该方法在进行规划过程中,起始点xstart和目标点xgoal在搜索空间中位置是已知的.在未有可行解存在的时候,该方法不断地在整个空间中批量均匀采样,并通过启发式的估计值递增地从xstart连接各采样点.当规划问题存在解时,由于批量采样均匀地逐渐覆盖整个搜索空间,最终xstart将通过采样点无碰撞地连接至xgoal,因此找到一条可行路径解的概率为1.基于上述论点,WB-BIT*具备概率完备性.
定理2 渐进最优性.当采样至无穷个样本时,WB-BIT*方法渐进收敛到给定路径规划问题的最优解的概率是1,即:
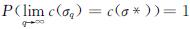 ,
,
其中:q是采样点的数量,σq是从这些采样点中找到的路径,c(σ*)代表理论最优路径长度.
证明 对于一个采样序列Xsamples={x1,x2,…,xq},WB-BIT*考虑了至少和RRT*相同的边和连接半径.RRT*从采样序列中的某个样本增量地构建一棵搜索树.该序列中的每个采样点xk∈Xsamples考虑了连接半径内的所有邻点:
Xnear,k={xj∈Xsamples|j<k,‖xk-xj‖2≤rRRT*}.
采样点xk从这些邻点中选择能够使得xk的当前实际gT(xk)最小化的状态进行连接,接着经重布线考虑其余邻点能否通过连接xk使各自当前gT(xother)降低.
给定相同的采样序列,WB-BIT*将采样序列分为批量样本,Xsamples={Y1,Y2,…,Yl}.其中每一批样本是q个采样点的集合,例如Y1={x1,x2,…,xq}.WB-BIT*通过处理该采样序列中每一批样本,递增地构建搜索树.对于集合y∈Yk中的每个采样点,均同时考虑了整个采样序列中处于连接半径内的所有邻点:
Xnear,k={x∈Yj|j<k,‖y-x‖2≤rBIT*}.
这些采样点通过与邻点的连接,将边添加到搜索树,使得当前实际gT最小化,并考虑连接范围内其余边连接至它的邻域.这组边的集合包含了RRT*在其连接范围内所考虑的所有边.给定RRT*连接半径:
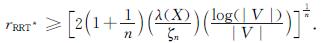 (4)
(4)
结合式(1)WB-BIT*方法的连接半径,由于WB-BIT*在任一批次样本中的连接半径与RRT*方法在该批次中第一个样本的连接半径相同,且两者的连接半径均单调递减,说明了WB-BIT*至少考虑和RRT*相同的边,同时WB-BIT*从这些边中选择能够降低搜索树中节点代价,并能够提供更好的路径连接.因此结合以上说明和Karaman等[10]对于RRT*渐进最优性能的论述,WB-BIT*也是具有渐进最优的性能.