《厦门大学学报（自然科学版）》

为了估算有黏流情况下飞艇的轴向附加质量系数,采用计算流体动力学(CFD)技术计算了有黏流情况下椭球体在时变来流速度下的气动力随时间变化曲线,然后通过傅里叶分析法辨识得到了椭球体的非定常气动力系数,最后将与加速度相关的气动力系数折算成轴向附加质量系数.通过研究相同空速下,来流速度对气动力的影响,将运动体在静止来流中运动的气动力计算问题转化为相同空速下运动体静止而来流时变的气动力计算问题.这种转化避免了在CFD计算中使用动网格技术.数值计算的结果表明:在一定的条件下,有黏流场中也可以定义轴向附加质量的概念; 但有黏流的轴向附加质量和无黏流中的结果有较大的差异.

To estimate the axial added mass(AAM)coefficient of the airship in viscous flow,we have computed the aerodynamic force of an ellipsoid suffered in a uniform but unsteady incoming flow based on CFD technology.The Fourier analysis method is then adopted to identify the unsteady aerodynamic force coefficient.At last,the acceleration-related aerodynamic coefficient is converted to AAM coefficient.By studying the effect of the incoming flow velocity on the aerodynamic force under the same airspeed,this computational problem of a solid moving in the fluid that rests at infinity is transformed into the case where the solid is stationary while the velocity of the incoming flow is time-varying.This transformation avoids adopting the dynamic mesh technology in CFD simulation.Numerical results show that,under certain conditions,the concept of AAM can also be defined in the viscous flow field.However,the AAM in viscous flows deviates from the corresponding result in potential flows distinctly.

引言
1 有黏流中的相对运动原理
2 轴向气动力附加质量辨识方法
3 有黏流场中椭球体的轴向附加质量系数特性分析
4 结论

图1 旋成椭球体的边界层网格<br/>Fig.1 Boundary layer grid of a rotating ellipsoid

图1 旋成椭球体的边界层网格
Fig.1 Boundary layer grid of a rotating ellipsoid

图2 旋成椭球体的整体网格<br/>Fig.2 The overall mesh of a rotating ellipsoid

图2 旋成椭球体的整体网格
Fig.2 The overall mesh of a rotating ellipsoid

图3 气动力F的拟合函数和原始数据<br/>Fig.3 Aerodynamic force's fitting function and raw data

图3 气动力F的拟合函数和原始数据
Fig.3 Aerodynamic force's fitting function and raw data

图4 k1,k2,k4,…,k9对应的项对气动力的贡献<br/>Fig.4 Influence of k1,k2,k4,…,k9's corresponding items on aerodynamic forces

图4 k1,k2,k4,…,k9对应的项对气动力的贡献
Fig.4 Influence of k1,k2,k4,…,k9's corresponding items on aerodynamic forces

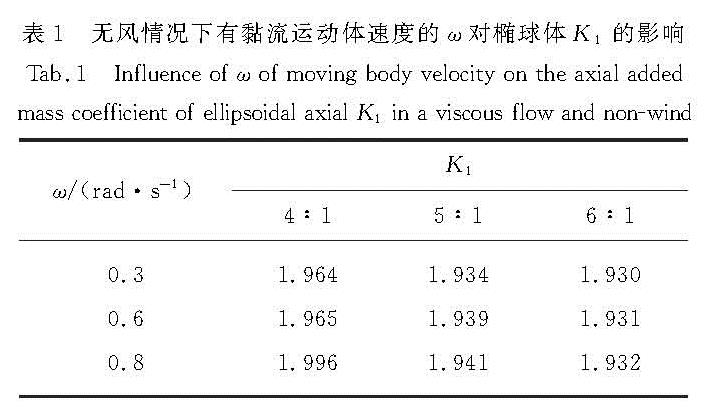
表1 无风情况下有黏流运动体速度的ω对椭球体K1的影响<br/>Tab.1 Influence of ω of moving body velocity on the axial added mass coefficient of ellipsoidal axial K1 in a viscous flow and non-wind

表1 无风情况下有黏流运动体速度的ω对椭球体K1的影响
Tab.1 Influence of ω of moving body velocity on the axial added mass coefficient of ellipsoidal axial K1 in a viscous flow and non-wind

表2 无风情况下有黏流运动体摄动速度的幅值A对椭球体K1的影响<br/>Tab.2 Influence of the amplitude A of the moving body'sperturbation velocity on the axial added mass coefficient of the ellipsoid K1 in a viscous flow and non-wind

表2 无风情况下有黏流运动体摄动速度的幅值A对椭球体K1的影响
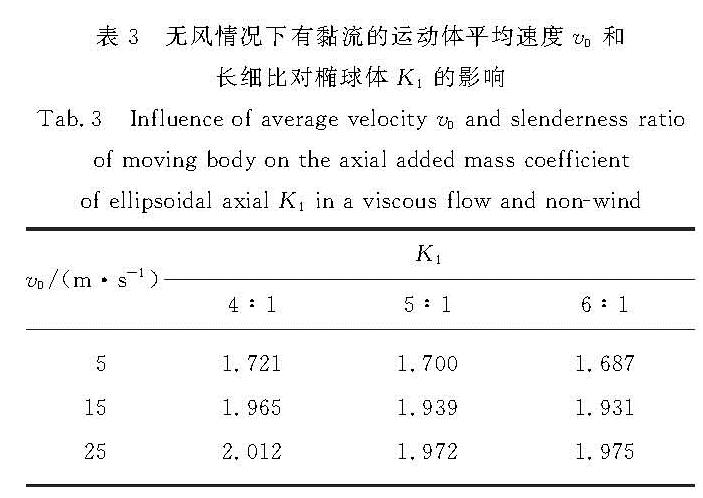
Tab.2 Influence of the amplitude A of the moving body'sperturbation velocity on the axial added mass coefficient of the ellipsoid K1 in a viscous flow and non-wind

表3 无风情况下有黏流的运动体平均速度v0和长细比对椭球体K1的影响<br/>Tab.3 Influence of average velocity v0 and slenderness ratioof moving body on the axial added mass coefficient of ellipsoidal axial K1 in a viscous flow and non-wind

表3 无风情况下有黏流的运动体平均速度v0和长细比对椭球体K1的影响
Tab.3 Influence of average velocity v0 and slenderness ratioof moving body on the axial added mass coefficient of ellipsoidal axial K1 in a viscous flow and non-wind

表4 无风情况下无黏流椭球体轴向附加质量系数<br/>Tab.4 Axial added mass coefficient of ellipsoid in a non-viscous flow and non-wind

表4 无风情况下无黏流椭球体轴向附加质量系数
Tab.4 Axial added mass coefficient of ellipsoid in a non-viscous flow and non-wind

[1] KHOURY G A,GILLETT J D.Airship technology[M].2nd ed.New York:Cambridge University Press,2012:36.
[2] Lamb H.Hydrodynamics [M].6th ed.New York:Dover,1945:160-201.
[3] TUCKERMAN L B.Inertia factors of ellipsoids for use in airship design,report No.210[R].Texas:Technical Report Archive and Image Library,1926.
[4] MUNK M M.The aerodynamic forces on airship hulls,report No.184[R].Seattce:National Advisory Committee for Aeronautics,1924.
[5] 方振平,陈万春,张曙光.航空飞行器飞行动力学[M].北京:北京航空航天大学出版社,2005:223.
[6] JONES S P,DELAURIER J D.Aerodynamic estimation techniques for aerostats and airship[J].Journal of Aircraft,2015,20(2):120-126.
[7] WANG X L.Computational fluid dynamics predictions of stability derivatives for airship[J].Journal of Aircraft,2012,49(3):933-940.
[8] CALERO J S.Jean le rond d'alembert:a new theory of the resistance of fluids[M].Berlin:Springer,2018:71.
[9] THOMASSON P G.Equations of motion of a vehicle in a moving fluid[J].Journal of Aircraft,2000,37(4):630-639.
[10] JOSÉ,AZINHEIRA R,PAIVA E C D,et al.Influence of wind speed on airship dynamics[J].Journal of Guidance Control & Dynamics,2002,25(25):1116-1124.
[11] WU J C.Elements of vorticity aerodynamics[M].Shanghai:Shanghai Jiaotong University Press,2014:55,77-94.
[12] 林献武,兰维瑶,李智斌,等.时变系统流场动量定理的积分形式及其在流体动力系数分析中的应用[J].应用数学和力学,2016,37(6):551-566.
[13] WU J Z,MA H Y,ZHOU M D.Vorticity and vortex dynamics[M].Berlin Heidelberg:Springer,2006:617-639.
[14] 林新武,林献武,兰维瑶.不可压缩流中飞艇艇体气动力的计算方法研究[D].厦门:厦门大学,2018:31-51.

备注

引言

1 有黏流中的相对运动原理

2 轴向气动力附加质量辨识方法

3 有黏流场中椭球体的轴向附加质量系数特性分析

4 结论

学报简介

备注

引言

1 有黏流中的相对运动原理

2 轴向气动力附加质量辨识方法

3 有黏流场中椭球体的轴向附加质量系数特性分析

4 结 论

学报简介

4 结论