(1.厦门大学信息科学与技术学院,福建 厦门 361005; 2.华南理工大学数学学院,广东 广州 510641)
稀疏表示; 非参数贝叶斯; Spike-Slab先验; 自适应字典; 语音增强
(1.School of Information Science and Engineering,Xiamen University,Xiamen 361005,China; 2.School of Mathematics,South China University of Technology,Guangzhou 510641,China)
sparse representation; nonparametric Bayesian estimation; Spike-Slab priori; dictionary learning; speech enhancement
DOI: 10.6043/j.issn.0438-0479.201611054
备注
提出一种基于非参数贝叶斯理论的语音增强算法,在稀疏表示的框架下,把字典学习、稀疏系数表示和噪声方差估计融合成一个贝叶斯后验估计的过程,并利用Spike-Slab先验加强稀疏性.首先,将带噪语音分解为干净语音、高斯噪声和残余噪声3个子信号,分别对该3种子信号采用不同的先验概率模型表达,接着采用马尔科夫链-蒙特卡洛算法计算出3个模型中每个参数对应的后验概率,最后基于稀疏表示的框架重构出干净语音.实验数据使用NOIZEUS语音库,采用PESQ和SegSNR作为质量评价指标,分别在信噪比为0,5和10 dB的高斯白噪声、火车噪声和街道噪声上验证了其可行性,并与多种常用语音增强方法进行对比,发现其在低信噪比非平稳噪声情况下的增强效果更为理想.
A new speech enhancement strategy is proposed by utilizing a nonparametric Bayesian method with Spike-Slab priori(NBSP).As a sparse representation framework,the dictionary learning,sparse coefficients representation and noise variance estimation are replaced by a single procedure of Bayesian posterior estimation.First,the noisy speech is divided into clean speech,Gaussian noise and rest noise.Then,each part is modeled with a certain priori distribution.Finally,upon the adoption of Markov Chain Monte Carlo sampling algorithm,the posterior distribution can be obtained,as the clean speech and all other parameters.Without knowing the noise variance,NBSPcould be performed directly on the noisy speech to infer the sparsity of the speech.Experiments were executed on NOIZEUS database.Experiments are executed on noisy speeches from NOIZEUS database with SNR ranging from 0 dB to 10 dB,which contain three types of noise(white,train and street).And the subjective and objective measures like PESQ score and the output SegSNR are implemented to evaluate the performance of NBSP and the other state-of-the-art methods.Corresponding results show that NBSP achieves better performances,especially in conditions of non-stationary noise with low input SNR.
引言
随着人工智能在日常应用的普及,语音已成为一种重要的人机交互手段,但在日常生活中,由于周围环境嘈杂及录音设备的干扰,语音信号经常携带有冗余的噪声,在一定程度上影响了人们的信息交流.因此,研究语音增强算法,以获取高自然度和清晰度的语音信号,是语音信号处理领域的热点问题之一.
从20世纪60年代起,研究者们提出了非常多的语音增强算法,常见有谱减法[1]、维纳滤波法[2]、小波阈值法[3]、子空间[4]、噪声估计[5-6]等.近几年来,基于稀疏表示理论的语音增强算法[7-11]受到越来越多的关注.稀疏表示理论以两个假设为前提,1)噪声信号与语音信号是不相关的,2)语音信号在过完备字典上的表示是稀疏的,因此字典的构建和目标函数的优化是基于稀疏表示理论的语音增强算法的两个重要部分.目前主要的字典构建方法有2种:1)固定字典法,该方法直接采用小波变换、离散余弦变换等方法生成字典的基底,运算量小,但无法自适应地表达不同的语音信号; 2)训练字典法,该方法采用如K空间的奇异值分解(K-SVD[7])这类的训练算法直接从样本数据中学得字典,这些字典原子更加符合信号本身的特性,但计算复杂,字典结构较为松散.不管是固定字典法还是传统的训练字典法,都需要使用者在训练字典时事先提供稀疏度或者误差阈值来决定字典的结构,然而在实际应用中较难满足上述条件,而不准确的稀疏度和误差阈值将导致不佳的增强效果.
受到非参数贝叶斯理论在图像去噪上成功应用[12]的启发,本研究将基于Spike-Slab先验的非参数贝叶斯(nonparametric Bayesian method based on Spike-Slab priori,NBSP)算法引入语音增强领域,采用基于非参数贝叶斯理论的字典学习方法进行语音信号的稀疏表示,并利用Spike-Slab先验[13-15]来加强稀疏表示结构中模型参数的稀疏性,以减少信号模型对参数的依赖程度.该模型假设带噪语音由干净语音、高斯噪声和残余噪声3个子信号相加而成,干净语音由字典和稀疏系数组成,接着对字典、稀疏系数、高斯噪声和残余噪声进行先验概率建模.假设其分别服从一定的先验分布,同时根据共轭先验分布对每个分布中的参数进行建模,其中稀疏系数和残余噪声服从Spike-Slab先验以加强稀疏性,最后采用马尔科夫链-蒙特卡洛算法[16-18]求得各个参数对应的后验概率,从而重构出干净噪声.
1 Spike-Slab先验
Spike-Slab先验[13-15]是一种稀疏先验,用来加强系数先验信息的稀疏性,一般由一个连续分布(如高斯分布)和一个δ分布混合而成,其中,连续分布为Slab项,δ分布为Spike项.狄拉克函数(Dirac Delta function,δ函数),亦称为单位脉冲函数,表示在零点处有值,其他点处为零的函数.该分布的结果具有严格的稀疏性,因此可以作为稀疏表示系数的先验信息来使用.Spike-Slab先验的一般形式为:
zk~(1-ωk)δ+ωkN(0,τ-1),
ωk~B(a,b),
其中,Spike项为δ分布,Slab 项为高斯分布,ωk为权重,服从超参数为a和b的Beta分布,ωk越小,其对应的系数就越有可能落入Spike 项,即zk越稀疏,因此ωk的取值可以控制系数的稀疏度.
2 基于Spike-slab先验的非参数贝叶斯算法
一条带噪语音可以表示为
x=s+ε,(1)
其中,x、s和ε分别表示时域上的带噪语音、干净语音和噪声.通常需对语音进行分帧处理,如把一条语音分成帧长为M的T帧,则每一帧语音可以表示为
xi=si+εi,i=1,…,T.(2)
在常用的稀疏表示方法中,用字典和稀疏系数的乘积来近似表示干净语音,即
si=(^overx)i=Dαi,(3)
其中,D={dk}Kk=1是由K个原子组成的字典,α={αi}Pi=1 是对应的稀疏系数.
另外,在实际应用中,εi可以表示为高斯噪声gi和残余噪声ri,因此有
xi=Dαi+gi+ri,(4)
本研究假设字典中的每一个原子dk之间是独立同分布的,并且都服从均值为0的高斯分布,即
dk~N(0,M-1IM),k=1,2,…,K,(5)
其中IM是维度为M×M的单位矩阵.
高斯噪声gi服从均值为0,方差为τ-1g IM的高斯分布,其中,τg为噪声精度,即噪声方差的倒数,服从超参数为u0和v0伽马分布,如下所示,
gi~N(0,τ-1gIM),
τg~Γ(u0,v0).(6)
考虑到稀疏系数和残余噪声的稀疏特性,假设两者都服从Spike-Slab先验,其中稀疏系数的表达如下所示:
αi~∏Kk=1[(1-πk)δ+πkΝ(0,τ-1α)],
πk~B(a0,b0),
τα~Γ(e0,f0);(7)
残余噪声的表示为
ri~∏Mm=1[(1-l)δ+lN(0,τ-1r)],
l~B(c0,d0),
τr~Γ(g0,h0),(8)
其中,参数πk表示对应的字典原子dk被用于表示重构语音的概率,参数l表示当前数据点为残余噪声的概率,τα和τr服从伽马分布,用于估计精度(方差的倒数).需要注意的是,语音信号x=[x1,x2,x3,…,xT]的所有帧共用一个字典D,因此与字典原子dk相关的参数πk也是所有帧共用的,而与残余噪声相关的参数l则不同,由于每个数据点为残余噪声的概率是相互独立的,因此一个数据点就对应着一个lim.
基于式(4)~(8)所有参数的先验概率模型,根据训练数据和贝叶斯推理,可以得到参数的后验概率分布.采用马尔科夫链-蒙特卡洛算法[28-30]计算模型的近似结果,如下:
1)字典原子dk概率分布:
P(dk〖JB<1|〗-)~N(μdk,σdk),(9)
其中,方差为σdk=(TIM+τg∑Ti=1α2ik )-1,均值为μdk=τgσdk∑Ti=1αik(xi-Dαi-si+dkαik).
2)稀疏系数αik的概率分布:
P(αik〖JB<1|〗-)~(1-(~overπ)k)δ(αik)+
(~overπ)kΝ(αik〖JB<1|〗(~overμ)αik,(~overσ)αik),(10)
其中,方差为(~overσ)αik=(τα+τgdTkdk)-1,均值为(~overμ)αik=τg(~overσ)αik[dTk(xi-Dαi-si+dkαik)],且有((~overπ)k)/(1-(~overπ)k)=(πk)/(1-πk)(N(0〖JB<1|〗0,τ-1α))/(N(0〖JB<1|〗(~overμ)αik,(~overσ)αik)).
3)概率参数πk的概率分布:
P(πk〖JB<1|〗-)~B(a0+∑Ti=11(αik≠0),b0+
∑Ti=11(αik=0)),(11)
其中,∑Ti=11(αik≠0)表示αik不等于0的个数,∑Ti=11(αik=0)表示αik等于0的个数.
4)精度τα的概率分布:
P(τα〖JB<1|〗-)~Γ(e0+1/2KT,f0+1/2∑Ti=1αTi αi).(12)
5)残余噪声rim的概率分布:
P(rim〖JB<1|〗-)~(1-(~overl))δ+(~overl)Ν(sim〖JB<1|〗(~overμ)sim,(~overσ)sim),(13)
其中,方差为(~overσ)sim=(τr+τg)-1,均值为(~overμ)sim=τg((~overσ)sim(^overε)im),且有((~overl))/(1-(~overl))=l/(1-l)(Ν(0〖JB<1|〗0,τ-1r))/(N(0〖JB<1|〗(~overμ)sim,(~overσ)sim)).
另外,在计算残余噪声之前,需要移除掉理想信号,因此有(^overε)i=xi-Dαi.
6)概率参数l的概率分布:
P(l〖JB<1|〗-)~B(c0+∑Mm=1∑Ti=11(rim≠0),d0+
∑Mm=1∑Ti=11(rim=0)),(14)
其中,∑Mm=1∑Ti=11(rim≠0)表示rim不等于0的个数,∑Mm=1∑Ti=11(rim=0)表示rim等于0的个数.
7)精度τr的概率分布:
P(τr〖JB<1|〗-)~Γ(g0+1/2MT,h0+1/2∑Ti=1rTiri).(15)
8)精度τg的概率分布:
P(τg〖JB<1|〗-)~Γ(u0+1/2MT,v0+
1/2∑Ti=1=xi-Dαi-ri=2).(16)
根据式(9)~(16),将所有的待求变量进行逐步迭代求解,在其他变量固定的前提下求解当前变量,然后对下一个变量进行上述相同操作,直至收敛到稳定状态(在后续实验中,根据实验经验设定迭代次数为100次),取稳定状态的D和α,根据式(3)重构出增强后的语音信号.
3 实验结果及分析
3.1 实验设置用于实验的30条干净语音来自NOIZEUS数据库[19].带噪语音由干净语音叠加噪声所得,信噪比分别为0,5和10 dB,噪声种类分别为高斯白噪声(WGN)、火车噪声和街道噪声,共270条.所有语音的采样率均为8 kHz,帧长M为128,帧移为1.初始字典大小K=1 024,考虑到实际使用的字典原子个数由数据本身决定,为了能更好地适应不同的语音数据,把初始字典大小设大一些.为了使先验信息对结果的影响尽可能的小,超参数取较小的值,如e0=f0=g0=h0=u0=v0=10-6[20].由于计算后验分布时,数据样本的影响远大于这些超参数,Spike-Slab先验中Beta分布的超参数a0,b0,c0和d0的选取对增强性能的影响较小,又因不同的取值影响着对应变量的初始稀疏度[15],且稀疏系数和残余噪声是稀疏的,因此取a0,b0,c0和d0的值分别为1,100T,0.1和0.9.
语音质量评价指标采用主观语音质量评价(PESQ)[21]和分段信噪比(SegSNR)Rseg,Rseg可用于衡量增强算法的去噪能力,PESQ是一种模拟人耳听觉感受的主观质量评价算法.实验结果均为30条语音的平均值,其中Rseg的公式如下:
Rseg=(10)/T∑Ti=1log(∑Mm=1s2im)/(∑Mm=1((^overx)ims2im)),(17)
3.2 与K-SVD算法的比较K-SVD算法作为稀疏表示算法中的典型算法,一直以来都受到学者们的广泛关注,其采用如下的目标优化函数
(^overα)=argminα‖α‖0+μ‖Dα-x‖22,(18)
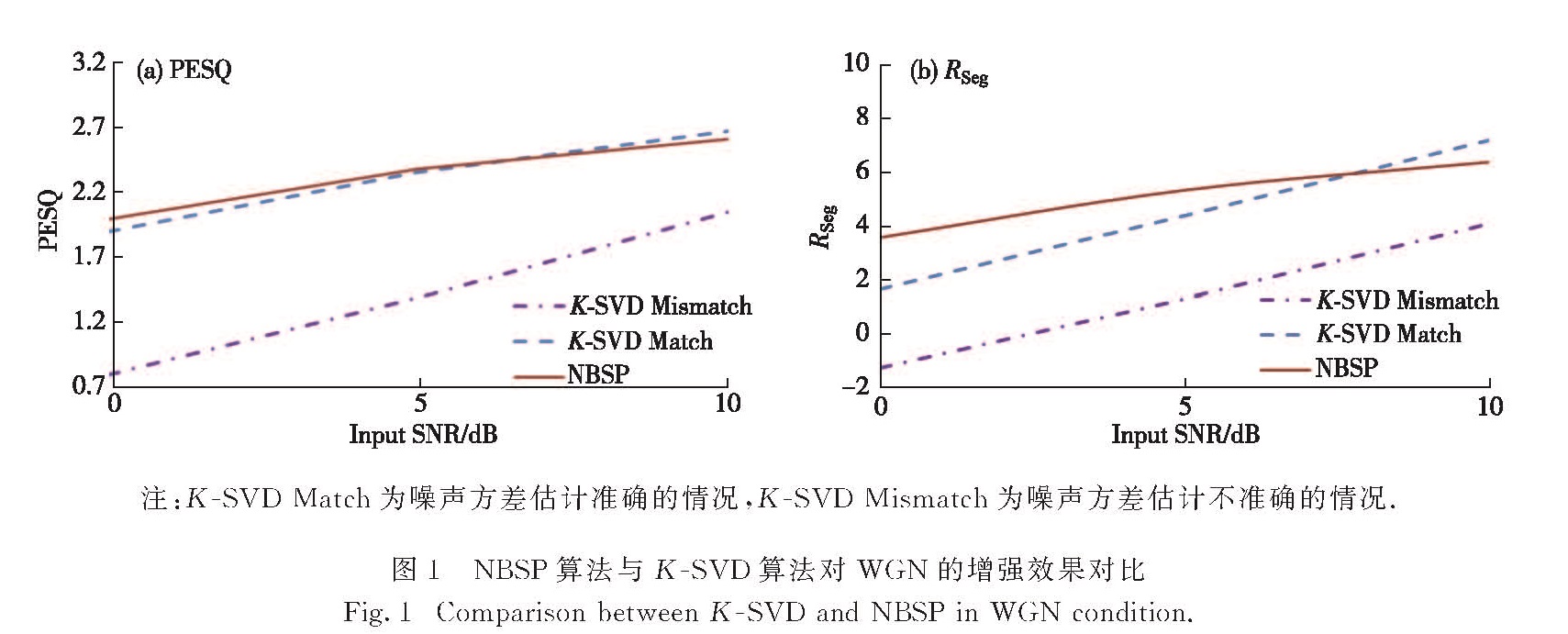
其中μ是权重.在满足‖α‖0≤L或‖Dα-x‖22≤σ的时候,迭代停止,因此需要事先给定一个稀疏度L或者一个阈值σ.尽管目前话音激活算法[22]可以用于估计噪声频谱,但在实际应用中要做到准确估计仍旧较难实现.而当噪声方差估计不准确时,K-SVD的结果会有非常明显的下降.图1给出了NBSP算法与K-SVD算法的对比结果.从图中可以看出,当噪声方差估计不准确(K-SVD Mismatch)时,K-SVD算法的结果会有明显的下降; 当噪声方差估计准确(K-SVD Match)时,NBSP与其性能相当.但值得注意的是,基于NBSP的语音增强方法不需要预先估计噪声方差,只需要对式(6)和(8)中的超参数设定一个初始值(具体见3.1实验设置),就可以通过数据本身和先验分布计算得到对应噪声精度(噪声方差的倒数)的后验分布,如式(15)和(16)所示,因此相比于K-SVD算法,该方法对参数的依赖性更低.
注:K-SVD Match为噪声方差估计准确的情况,K-SVD Mismatch为噪声方差估计不准确的情况.
3.3 与常用语音增强算法的比较为了进一步探究NBSP算法的有效性,本节把NBSP算法同目前常用的几种语音增强算法进行了对比,结果如表1所示.主要有谱减法(SS)[1]、维纳(Wiener)滤波法[2]、子空间(subspace)[4]、使用非因果先验的最小化均方误差算法(MMSE_NPS)[5]、基于估计频谱幅值平方最大后验的增强算法(MSS_MAP)[6]和基于低秩约束的稀疏矩阵分解法(CLSMD)[11],对比数据使用的是参考文献[11]中的实验结果.由表1可知,NBSP方法在处理低信噪比非平稳噪声的带噪信号时,具有较大的优势.当带噪语音信噪比为0和5 dB时,NBSP的Rseg除了在0 dB火车噪声情况下略低于CLSMD方法外,其他情况下均取得了最大值,这说明NBSP方法在低信噪比情况下去除噪声的能力强,且在5 dB街道噪声时,NBSP的Rseg比排名第二的CLSMD提升了约125%; 从PESQ的值来看,NBSP方法均取得了最高值,仅在5 dB火车噪声情况和0 dB街道噪声情况下其PESQ值分别与CLSMD方法和MMSE_NPS方法持平.当带噪语音信噪比为10 dB时,尽管NBSP的Rseg和PESQ值相对其他算法不是最高值,但也与最大值相差不大.因此在10 dB带噪信号情况下,NBSP方法具有比较稳定的增强性能.NBSP方法的2种评价指标均取得不错结果,说明该方法在低信噪比情况下不仅去噪能力强,而且增强后的语音拥有着良好的听觉效果,而目前大多算法都偏向某一个指标的优势,很难实现二者的均衡,尤其是在针对非平稳噪声情况下,如街道噪声.
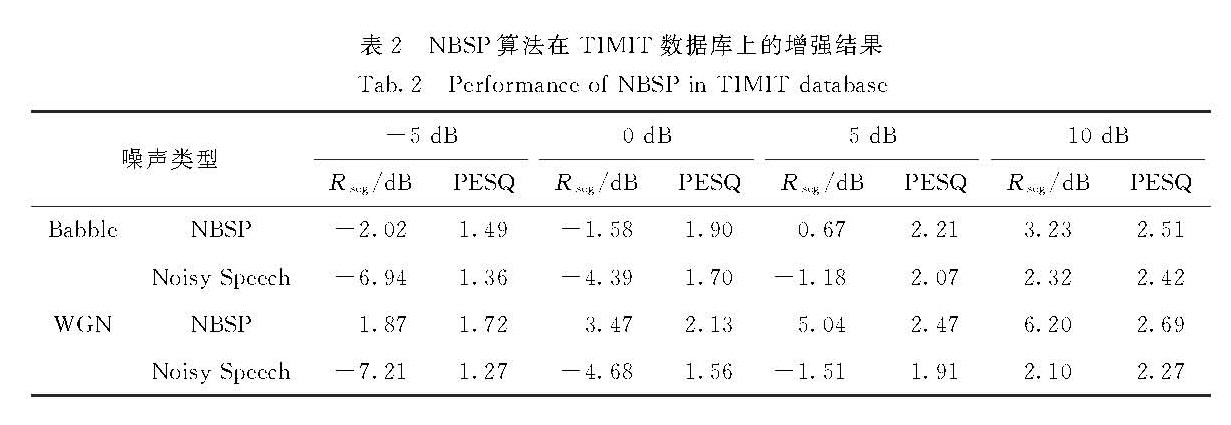
另外,为了探究NBSP方法在不同数据库以及更多噪声上的适应性,选取TIMIT数据库[23]中的20条不同语音(男女比例1:1,每人一条语音), 分别叠加来
注:加粗为最优结果.
自Noisex92噪声库[24]的WGN和Babbe噪声,噪声强度为-5,0,5和10 dB,所有语音的采样率均为16 kHz.用NBSP方法进行增强,结果如表2所示,从表中数据可以看出,NBSP方法在TIMIT数据库上的有效性.
4 结 论
在稀疏表示框架下,引入了NBSP.该算法不需要预先设定约束项或者稀疏度,可直接从数据本身学得字典、干净语音、噪声方差等参数.除此之外,基于非参数贝叶斯理论的字典学习方法可以直接对单条语音进行处理,不需要利用其他数据提前训练字典.实验结果表明了该方法的可行性,尤其在低信噪比非平稳噪声情况下具有较大的优势.但不足之处在于,该方法与其他稀疏表示方法一样具有较高的计算复杂度,不适用于实时处理应用场景.
- [1] BOLL,S.Suppression of acoustic noise in speech using spectral subtraction[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1979,27(2):113-120.
- [2] SCALART,P.Speech enhancement based on a priori signal to noise estimation[C]∥1996 IEEE International Conference on Acoustics,Speech,and Signal Processing(ICASSP).Atlanta,Georgia:IEEE,1996:629-632.
- [3] VETTERLI M.Wavelets,approximation,and compression[J].IEEE Signal Processing Magazine,2001,18(5):59-73.
- [4] DE M B.The singular value decomposition and long and short spaces of noisy matrices[J].IEEE Transactions on Signal Processing,1993,41(9):2826-2838.
- [5] COHEN I.Speech enhancement using a noncausal a priori SNR estimator[J].IEEE Signal Processing Letters,2004,11(9):725-728.
- [6] LU Y,LOIZOU P C.Estimators of the magnitude-squared spectrum and methods for incorporating SNR uncertainty[J].IEEE Transactions on Audio,Speech,and Language Processing,2011,19(5):1123-1137.
- [7] ZHAO N,XU X,YANG Y.Sparse representations for speech enhancement[J].Chinese Journal of Electronics,2011,19(2):268-272.
- [8] MOHAMMADIHA N,SMARAGDIS P,LEIJON A.Supervised and unsupervised speech enhancement using nonnegative matrix factorization[J].IEEE Transactions on Audio,Speech,and Language Processing,2013,21(10):2140-2151.
- [9] SIGG C D,DIKK T,BUHMANN J M.Speech enhancement using generative dictionary learning[J].IEEE Transactions on Audio,Speech,and Language Processing,2012,20(6):1698-1712.
- [10] BABY D,VIRTANEN T,BARKER T.Coupled dictionary training for exemplar-based speech enhancement[C]∥2014 IEEE International Conference on Acoustics,Speech and Signal Processing(ICASSP).Florence,Italy:IEEE,2014:2883-2887.
- [11] SUN C,ZHU Q,WAN M.A novel speech enhancement method based on constrained low-rank and sparse matrix decomposition[J].Speech Communication,2014,60(5):44-55.
- [12] ZHUANG P,HUANG Y,ZENG D,et al.Mixed noise removal based on a novel non-parametric Bayesian sparse outlier model[J].Neurocomputing,2016,174:858-865.
- [13] MITCHELL T J,BEAUCHAMP J J.Bayesian variable selection in linear regression[J].Journal of the American Statistical Association,1988,83(404):1023-1032.
- [14] GEORGE E I,MCCULLOCH R E.Variable selection via Gibbs sampling[J].Journal of the American Statistical Association,1993,88(423):881-889.
- [15] DING X,MI Z,HUANG Y,et al.Robust RVM based on spike-slab prior[J].Journal of Electronics(China),2012,29(6):593-597.
- [16] HAMMERSLEY J M,HANDSCOMB D C.Monte Carlo methods[M].London:Chapman and Hall,2013.
- [17] JACKMAN S.Estimation and inference via Bayesian simulation:an introduction to Markov chain Monte Carlo[J].American Journal of Political Science,2000,44(44):375-404.
- [18] SUN S.A review of deterministic approximate inference techniques for Bayesian machine learning[J].Neural Computing and Applications,2013,23(7):2039-2050.
- [19] HU Y,LOIZOU P C.Subjective comparison of speech enhancement algorithms[C]∥2006 IEEE International Conference on Acoustics,Speech and Signal Processing(ICASSP).Toulouse:IEEE,2006:I153-I156.
- [20] TIPPING M E.Sparse Bayesian learning and the relevance vector machine[J].Journal of Machine Learning Research,2001,1(3):211-244.
- [21] RIX A W,BEERENDS J,HOLLIER M,et al.Perceptual evaluation of speech quality(PESQ),an objective method for end-to-end speech quality assessment of narrowband telephone networks and speech codecs:P862[S].Geneva:ITU-T Recommendation,2001:1-19.
- [22] TASHEV I,LOVITT A,ACERO A.Unified framework for single channel speech enhancement[C]∥2009 IEEE Pacific Rim Conference on Communications,Computers and Signal Processing.Victoria,BC:IEEE,2009:883-888.
- [23] GAROFOLO J S.Getting started with the DARPA TIMIT CD-ROM:An acoustic phonetic continuous speech database[R].Gaithersburgh,MD:National Institute of Standards and Technology(NIST),1988.
- [24] VARGA A,STEENEKEN H J M.Assessment for automatic speech recognition:II.NOISEX-92:A database and an experiment to study the effect of additive noise on speech recognition systems[J].Speech Communication,1993,12(3):247-251.